Diszkrimináns elemzés

A diszkriminancia analízis egy módszer a többváltozós eljárás a statisztikák , és arra szolgál, hogy különbséget a két vagy több csoport, amelyek leírása több (szintén változók). Ennek során ellenőrizheti a csoportok jellemzőinek jelentős különbségeit, és azonosíthatja a megfelelő vagy alkalmatlan jellemzőket. RA Fisher először 1936-ban írta le : Többszörös mérések alkalmazása taxonómiai problémákban .

A diszkrimináns elemzést a statisztikákban és a gépi tanulásban használják annak érdekében , hogy a térbeli transzformáció révén a jellemzőket jól ábrázolják, és osztályozóként ( diszkrimináns függvényként ) vagy dimenziócsökkentésként szolgál. A diszkrimináns elemzés kapcsolódik a főkomponens-elemzéshez (PCA), amelynek szintén jó reprezentációs lehetőséget kell találnia, de ezzel szemben figyelembe veszi az adatok osztálybeli hovatartozását.

Probléma

Olyan objektumokat tekintünk, amelyek mindegyike pontosan több hasonló osztály egyikébe tartozik. Ismert, hogy az egyes objektumok melyik osztályba tartoznak. Megfigyelik az egyes objektumok jellemzőit. Ezekből az információkból meg kell találni az osztályok közötti lineáris határokat annak érdekében, hogy később olyan objektumokat lehessen hozzárendelni, amelyek osztálytagsága ismeretlen az egyik osztály számára. A lineáris diszkrimináns elemzés tehát osztályozási módszer .

Példák:

• A hitelfelvevők pl. B. hitelképesre és nem hitelképesre kell osztani. Amikor egy banki ügyfél hitelt igényel, a bank olyan jellemzők alapján próbálja meghatározni az ügyfél jövőbeni fizetőképességét és fizetési hajlandóságát, mint a jövedelemszint, a hitelkártyák száma, az utolsó munkahelyen töltött munkaviszony időtartama stb.
• A szupermarketlánc vásárlói besorolhatók márka- és nem névvásárlók közé. Lehetséges jellemzők a teljes éves kiadás ezekben az üzletekben, a márkás termékek aránya a kiadásokban stb.

Legalább egy statisztikai, metrikusan méretezett jellemző figyelhető meg ezen az objektumon . Ezt a tulajdonságot véletlen változóként értelmezik a diszkrimináns elemzés modelljében . Legalább két különböző csoport létezik (populációk, általános populációk ). Az objektum ezen populációk egyikéből származik. Az objektumot egy hozzárendelési szabály, az osztályozási szabály segítségével hozzárendelik ezen alapcsoportok egyikéhez. Az osztályozási szabályt gyakran megkülönböztető függvény adhatja meg . ${\ displaystyle X}$ ${\ displaystyle X}$

Osztályozás ismert eloszlási paraméterekkel

A jobb megértés érdekében az eljárást példákkal magyarázzák.

Maximális valószínűség módszer

A hozzárendelés egyik módszere a maximális valószínűség módszer: az objektum ahhoz a csoporthoz van hozzárendelve, amelynek a valószínűsége a legnagyobb.

Egy jellemző - két csoport - egyenlő eltérések

példa

Az óvodának lehetősége van olcsón megvásárolni egy bizonyos fajta szegfűszeg nagyszámú magját. Annak a gyanúnak a feloszlatása érdekében, hogy régi, egymásra borított magról van szó, csíratesztet hajtanak végre. Tehát elvet 1 g magot, és megszámolja, hány ilyen mag csírázik. Tapasztalatból ismert, hogy az 1 g magra jutó csírázó magok száma szinte normálisan oszlik meg . Friss magokkal (I. populáció) átlagosan 80 mag csírázik, a régiekkel (II. Populáció) csak 40 mag.

• I. populáció: A csírázó friss magok száma eloszlik ${\ displaystyle X_ {I} \ sim N (80; 10 ^ {2}),}$
• II. Populáció: A csírázó régi magok száma eloszlik ${\ displaystyle X_ {II} \ sim N (40; 10 ^ {2}),}$

A csíra minta most

${\ displaystyle x = 70}$

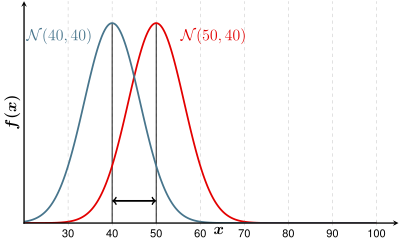
megadás. A grafika azt mutatja, hogy ennél a mintánál az I populáció valószínűsége a legnagyobb. Tehát ezt a csíramintát frissnek minősíti.

A grafikon azt mutatja, hogy osztályozási szabályként ( döntési szabályként ) is megadhatja:

Rendelje az objektumot az I populációhoz, ha a várható értéktől a legkisebb a távolság , vagy ha ${\ displaystyle x}$ ${\ displaystyle \ mu _ {I}}$

${\ displaystyle | x- \ mu _ {I} | <| x- \ mu _ {II} |}$

van.

Az eloszlási sűrűségek metszéspontja (at ) tehát megfelel a döntési határnak. ${\ displaystyle x = 60}$

A jellemzők kívánatos eloszlási tulajdonságai

Ugyanazok a szórások

A két csoport jellemzőinek azonos szórással kell rendelkezniük . Különböző eltérésekkel több hozzárendelési lehetőség létezik.

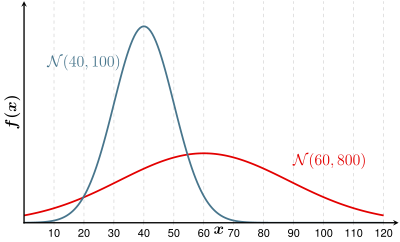
A fenti grafikonon két különböző eltérésű csoport látható. A lapos normális eloszlás nagyobb szórással rendelkezik, mint a keskeny, magas. Látható, hogy az I. csoport varianciája „miként ássa alá” a II. Csoport normális eloszlását. Ha például a minta eredménye lenne, a magokat frissnek kellene minősíteni, mivel az I. csoport valószínűségi sűrűsége nagyobb, mint a II. ${\ displaystyle x = 10}$

A diszkriminanciaanalízis „standard modelljében” ugyanazokat a varianciákat és kovarianciákat feltételezzük.

Nagy csoportok közötti eltérés

A változás között a csoport átlagértékek , a csoportközi variancia , nagynak kell lennie, mert akkor az eloszlások nem keveredik: a szétválasztás a csoportok élesebb.

Kis csoporton belüli variancia

A variancia belül egy csoport, az intra- csoport variancia , legkisebbnek kell lennie, amennyire csak lehetséges, akkor az eloszlások nem keverjük össze, az elválasztás jobb.

Több funkció - két csoport - ugyanazok a kovariancia mátrixok

Az érdeklődés tárgyának számos megfigyelhető vonása lehet . Itt véletlenszerű vektort kapunk mint modelleloszlás-struktúrát . Ez a vektor eloszlik a várható értékvektorral és a kovariancia mátrixszal . A konkrét megvalósítás a jellemzővektor , amelynek összetevői tartalmazzák az egyes jellemzőket . ${\ displaystyle x_ {j} (j = 1, \ pont, m)}$ ${\ displaystyle X}$ ${\ displaystyle \ mu}$ ${\ displaystyle \ Sigma}$${\ displaystyle x}$${\ displaystyle x_ {j}}$

Abban az esetben, két csoport, analóg módon a fenti, a megfigyelt objektum van hozzárendelve a csoport, amelyben az közötti távolság a jellemző vektor , és a várható érték vektor minimális. A Mahalanobis távolságot itt használjuk, részben átalakítva, a távolság méréseként . ${\ displaystyle x}$

példa

Egy nagy vidámparkban meghatározzák a látogatók költekezési szokásait. Különösen az érdekli őket, hogy a látogatók egy park tulajdonában lévő szállodában töltik-e az éjszakát. Minden család teljes költségei (jellemző ) és az ajándéktárgyak költségei (jellegzetes ) 16 óráig tartanak. A marketing menedzsment sok éves tapasztalat alapján tudja, hogy a megfelelő véletlen változók és együttesen megközelítőleg normálisan vannak elosztva a 25 [ ² ] és a kovariancia [ ² ] varianciákkal . A szállodai foglalások tekintetében a fogyasztókat költési magatartásuk alapján két I. és II. Csoportba sorolhatjuk, hogy az ismert megoszlási paraméterek a következő táblázatban szerepeljenek: ${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$${\ displaystyle X_ {1}}$${\ displaystyle X_ {2}}$${\ displaystyle Cov_ {12} = 20}$

csoport	Teljes kiadás	Emléktárgyak kiadása
	Várható érték ${\ displaystyle E (X_ {1})}$	Várható érték ${\ displaystyle E (X_ {2})}$	Varianciák és${\ displaystyle X_ {1}}$${\ displaystyle X_ {2}}$
Szállodafoglaló I	70	40	25-én
Nincs szállodafoglaló II	60	20	25-én

Az I. csoportnál a véletlenszerű vektor többváltozós, normálisan eloszlatva a várt értékvektorral

${\ displaystyle \ mu _ {I} = {\ kezdés {pmatrix} 70 \\ 40 \ end {pmatrix}}}$

és a kovariancia mátrix

${\ displaystyle \ Sigma _ {I} = {\ kezdés {pmatrix} 25 & 20 \\ 20 & 25 \ end {pmatrix}}}$

Ugyanez vonatkozik a II. Csoportra is.

A két csoport populációit az alábbi ábra sűrű pontfelhőként jelöli. Az ajándéktárgyakra fordított kiadásokat luxuskiadásoknak nevezik. A rózsaszínű pont az első csoport várható értékét jelenti, a világoskék a II.

Egy másik család meglátogatta a vidámparkot. Összesen 65 eurót költött 16 óráig és 35 eurót ajándéktárgyakra (zöld pont a grafikán). Készen állna egy szállodai szobára ennek a családnak?

Egy pillantás a grafikára már azt sugallja, hogy a zöld pont és az I. csoport várható értékvektora közötti távolság minimális. Ezért a szálloda vezetése gyanítja, hogy a család szobát fog venni.

A Mahalanobis távolságra

${\ displaystyle d_ {I} (x) = d (x, \ mu _ {I}) = (x- \ mu _ {I}) ^ {T} \ Sigma ^ {- 1} (x- \ mu _ {ÉN}).}$

A funkció vektor , hogy a központ I. csoport számítjuk ${\ displaystyle x}$

${\ displaystyle d_ {I} (x) = {\ elején {pmatrix} 65-70; & 35-40 \ vége {pmatrix}} {\ elején {pmatrix} 0 {,} 111 és -0 {,} 089 \ \ - 0 {,} 089 és 0 {,} 111 \ end {pmatrix}} {\ begin {pmatrix} 65-70 \\ 35-40 \ end {pmatrix}} = 1 {,} 11}$

és a II. csoport központjáig ${\ displaystyle x}$

${\ displaystyle d_ {II} (x) = {\ elején {pmatrix} 65-60; & 35-20 \ vége {pmatrix}} {\ elején {pmatrix} 0 {,} 111 és -0 {,} 089 \ \ - 0 {,} 089 és 0 {,} 111 \ end {pmatrix}} {\ begin {pmatrix} 65-60 \\ 35-20 \ end {pmatrix}} = 14 {,} 44.}$

Több funkció - több csoport - ugyanazok a kovariancia mátrixok

Az elemzés több mint két populáción alapulhat. Itt is, a fentihez hasonlóan, az objektumot hozzárendelik ahhoz a populációhoz, amelyben a jellemző vektor Mahalanobis távolsága a várt értékvektortól minimális. ${\ displaystyle x}$

(Halász) diszkriminatív funkciója

A gyakorlatban nehéz besorolni a Mahalanobis-távolságot minden osztályozandó tulajdonságra. A hozzárendelés lineáris diszkrimináns függvény segítségével könnyebb . A döntési szabály alapján

"Rendelje hozzá az objektumot az I. csoporthoz, ha az objektum és az I. csoport közötti távolság kisebb":

${\ displaystyle d_ {II} (x)> d_ {I} (x)}$

Ezen egyenlőtlenség átalakításával a döntési szabály a diszkrimináns függvény segítségével jön létre : ${\ displaystyle f (x)}$

"Az objektum hozzárendelése az I. csoporthoz, ha az alábbiak érvényesek":

${\ displaystyle f (x)> 0}$.

A diszkrimináns függvényt két csoport és ugyanazok a kovarianciamátrixok esetében számoljuk ki, mint

${\ displaystyle f (x) = (x - {\ tfrac {1} {2}} (\ mu _ {I} + \ mu _ {II})) ^ {T} \ Sigma ^ {- 1} (\ mu _ {I} - \ mu _ {II}) = {\ tfrac {1} {2}} (d_ {II} (x) -d_ {I} (x))}$

A diszkrimináns függvény empirikus megközelítésként is eredményez, ha valaki maximalizálja a csoportok közötti varianciát és minimalizálja a csoportokon belüli varianciát. Ezt a megközelítést Fisher diszkriminatív funkciójának hívják, mert RA Fisher vezette be 1936-ban.

Bayesi diszkrimináns elemzés

Eddig azt a feltételezést tették, hogy a populáció csoportjai azonos méretűek. De ez nem szokás. A csoporthoz való tartozás véletlenszerűnek is tekinthető. Azt a valószínűséget, amellyel egy objektum egy csoporthoz tartozik, a priori valószínűségnek nevezzük . Abban az esetben, csoportok, a lineáris diszkrimináns szabály azon a feltételezésen alapul, hogy a csoport egy többváltozós normális eloszlást egy várható érték és kovariancia mátrix , ami ugyanaz, minden csoportban, vagyis a H. . Ezután a lineáris diszkrimináns elemzésre (LDA) vonatkozó Bayes-szabály olvasható ${\ displaystyle i}$${\ displaystyle \ pi _ {i}}$${\ displaystyle K}$${\ displaystyle X}$${\ displaystyle i}$${\ displaystyle \ mu _ {i}}$${\ displaystyle \ Sigma}$${\ displaystyle X \ sim N (\ mu _ {i}, \ Sigma)}$

${\ displaystyle \ delta ^ {*} (x) = arg \ min _ {j \ in \ {1, ..., K \}} \ sum _ {i = 1, i \ neq j} ^ {K} [\ log (c_ {j | i}) + \ log (\ pi _ {i}) + x ^ {T} \ Sigma ^ {- 1} \ mu _ {i} - {\ frac {1} {2 }} \ mu _ {i} ^ {T} \ Sigma ^ {- 1} \ mu _ {i}],}$

ahol azt a költséget jelöli, amely akkor merül fel, ha az i csoporthoz tartozó objektumot tévesen hozzárendelik a j csoporthoz. ${\ displaystyle c_ {j | i}}$

Ha nem feltételezzük a fenti modellben, hogy a kovarianciamátrixok a csoportokban azonosak, de eltérhetnek, azaz H. , ez Bayes szabálya a másodfokú diszkrimináns elemzéshez (QDA) ${\ displaystyle X \ sim N (\ mu _ {i}, \ Sigma _ {i})}$

${\ displaystyle \ delta ^ {*} (x) = arg \ min _ {j \ in \ {1, ..., K \}} \ sum _ {i = 1, i \ neq j} ^ {K} [\ log (c_ {j | i}) + \ log (\ pi _ {i}) - {\ frac {1} {2}} \ log | \ Sigma _ {i} | - {\ frac {1} {2}} (x- \ mu _ {i}) ^ {T} \ Sigma _ {i} ^ {- 1} (x- \ mu _ {i})].}$

A lineáris diszkrimináns elemzéskor a határértékek lineárisak , a másodfokú másodfokúak. ${\ displaystyle x}$

Lásd még: Bayesi osztályozó

Besorolás ismeretlen eloszlási paraméterekre

A mögöttes jellemzők eloszlása ​​legtöbbször ismeretlen lesz. Tehát értékelni kell. Mindkét csoportból úgynevezett tanulási mintát veszünk, amennyiben ill . Ezzel az információval becsülték a várható értékvektorokat és a kovarianciamátrixot . A fenti esethez hasonlóan a Mahalanobis-távolságot vagy a diszkrimináns függvényt alkalmazzuk, a valós paraméterek helyett becsült értékkel. ${\ displaystyle n_ {I}}$${\ displaystyle n_ {II}}$${\ displaystyle \ mu _ {i} (i = I, II)}$ ${\ displaystyle \ Sigma _ {i}}$

Feltételezve, hogy a standard modell csoportszerű kovariancia mátrixokkal rendelkezik, a kovariancia mátrixok egyenlőségét először Box M tesztjének segítségével kell megerősíteni .

példa

Vidámparki példa felülről:

A lakosság ma ismeretlen. Minden csoport 16 családját vizsgálták meg alaposabban. Az alábbi értékek eredményezték a mintát:

Családok kiadásai egy vidámparkban
1. csoport			2. csoport
teljes	Ajándéktárgyak	csoport	teljes	Ajándéktárgyak	csoport
64,78	37.08	1	54,78	17.08	2
67.12	38.44	1	57.12	18.44	2
71.58	44.08	1	61.58	24.08	2
63.66	37.40	1	53.66	17.40	2
53.80	19.00	1	43.80	7.99	2
73.21	41.17	1	63.21	29.10	2
63,95	31.40	1	53,95	11.40	2
78.33	45,92	1	68.33	34.98	2
72.36	38.09	1	62.36	18.09	2
64.51	34.10	1	54.51	14.10	2
66.11	34.97	1	56.11	14,97	2
66.97	36.90	1	56.97	16.90	2
69,72	41.24	1	59,72	21.24	2
64.47	33.81	1	54.47	13.81	2
72,60	19.05	1	62,60	30.02	2
72.69	39.88	1	62.69	19.88	2

Az egyes csoportok átlagát, a teljes átlagot, a kovariancia mátrixokat és az egyesített (összesített) kovarianciát a következőképpen számoltuk:

változó	Összevont átlag	Azt jelenti
		1. csoport	2. csoport
teljes	62.867	67.867	57.867
ajándéktárgy	27,562	35.783	19,342

Összevont kovariancia mátrix
	teljes	ajándéktárgy
teljes	32.59
ajándéktárgy	30.58	54.01

Kovariancia mátrix az 1. csoport számára
	teljes	ajándéktárgy
teljes	32.59
ajándéktárgy	25.34	56.90

Kovariancia mátrix a 2. csoport számára
	teljes	ajándéktárgy
teljes	32.59
ajándéktárgy	35.82	51.11

Ebből kapjuk meg a fenti képlet alapján a diszkrimináns függvényt

${\ displaystyle f (x) = - 4 {,} 690 + 0 {,} 020 \ cdot {\ text {Total}} + 0 {,} 124 \ cdot {\ text {Souvenir}}}$.

A besorolási szabály most:

Rendelje az objektumot az I. csoporthoz, ha

${\ displaystyle f (x)> 0}$

van.

A minta értékei osztályozhatók a modell minőségének ellenőrzése érdekében. Az osztályozási mátrix itt adódik

csoport	Helyesen van hozzárendelve	helytelenül van hozzárendelve
ÉN.	14-én	2
II	13.	3

Most újra meg kell rendezni a megfigyeléssel rendelkező családot . ${\ displaystyle (65; 35)}$

Az alábbi ábra a tanulási minta szórási diagramját mutatja a csoportos eszközökkel. A zöld pont az objektum helye . ${\ displaystyle (65; 35)}$

A grafika már mutatja, hogy ez az objektum az I. csoporthoz tartozik. A diszkrimináns függvény megadja

${\ displaystyle f (x) = - 4 {,} 690 + 0 {,} 020 \ szor 65 + 0 {,} 124 \ szor 35 = 0 {,} 967.}$

Ott

${\ displaystyle f (x)> 0}$

az objektum az I. csoporthoz van hozzárendelve.

További kulcsszavak

• Wilks Lambda
• Rugalmas diszkrimináns elemzés
• Kernel sűrűségbecslő
• Támogatja a vektor gépet

irodalom

• Maurice M. Tatsuoka: Többváltozós elemzés: technikák az oktatási és pszichológiai kutatáshoz. John Wiley & Sons, Inc., New York, 1971, ISBN 0-471-84590-6
• KV Mardia, JT Kent, JM Bibby: Többváltozós elemzés . New York, 1979
• Ludwig Fahrmeir, Alfred Hamerle, Gerhard Tutz (szerk.): Többváltozós statisztikai módszerek . New York, 1996
• Joachim Hartung , Bärbel Elpelt: Többváltozós statisztika . München, Bécs, 1999
• Backhaus, Klaus; Erichson, Bernd; Plinke, Wulff és mtsai: Többváltozós elemzési módszerek.

web Linkek

• Springer Matematika Enciklopédia: Diszkrimináns elemzés

Egyéni bizonyíték

1. ↑ Klaus Backhaus, SpringerLink (online szolgáltatás): Többváltozós elemzési módszerek alkalmazásorientált bevezetés . Springer, Berlin 2006, ISBN 978-3-540-29932-5 .
2. ↑ RA Fisher (1936), Többféle mérés alkalmazása taxonómiai problémákban , Annals Eugen., 7. kötet, 179–188., Doi : 10.1111 / j.1469-1809.1936.tb02137.x