Hiperbolikus geometria

A négyzet alakú sík csempézésének modellje . Több mint négyen találkoznak a sarkokban (mérettől függően itt öt).

A hiperbolikus geometria (más néven Lobachevskian geometria vagy Lobachevsky geometria ) egy példa egy nem euklideszi geometriára , amelyet akkor kapunk, ha az abszolút geometria axiómáihoz hozzáadjuk az ellentmondó hiperbolikus axiómát az euklideszi geometriákat jellemző párhuzamok axiómája helyett . Ez azt jelenti, hogy egy g egyenes és egy P pont (amely nem fekszik a g-n ) esetében nem csak egy van, mint az euklideszi geometriában, hanem legalább két egyenes ( h és i ), amelyek átmennek P-n és párhuzamosak az g . Az a tény, hogy két egyenes „párhuzamos” egymással, csak azt jelenti, hogy ugyanabban a síkban fekszenek, és nincsenek közös pontjaik, és nem azt, hogy mindenhol azonos távolságúak legyenek ( h és én csak egy közös P pont van ).

Belátható, hogy bármely egyenes g bármilyen ponton kívül g vannak végtelen sok nem metsző vonalak ( „párhuzamot”), amely síkban fekszenek által meghatározott pont és a vonal. Kettő közülük a borderline helyzetben, és az úgynevezett határ- párhuzamos (még: horoparallel) az egyenes vonalat, míg a fennmaradó egyenes vonalak nevezik superparallel (még: hyperparallel).

A valódi hiperbolikus sík ábrázolása

A valódi hiperbolikus sík többféleképpen jeleníthető meg a valódi euklideszi síkon. Ezek többségét magasabb dimenziókra lehet általánosítani.

Ezen módszerek mindegyikén ugyanaz az elvont hiperbolikus geometria jelenik meg: a valódi hiperbolikus sík. Ezért lehetséges az ábrázolások és az állítások konvertálása pusztán hiperbolikus geometriában, függetlenül az alkalmazott "modelltől". A matematikában általában különböző modellekről beszélünk, ha két nem izomorf struktúra kielégíti ugyanazt az axiómarendszert. Ebben a tekintetben a következő „modellek” ugyanazt a szerkezetet írják le, tehát csak egy modell különböző ábrázolásai. Ezeket az ábrázolásokat azonban a szakirodalomban mindig modellként említik, és ez itt is érvényes. Más testek fölötti hiperbolikus síkok és több mint kétdimenziós hiperbolikus terek: lásd Metrikus abszolút geometria .

Körlemez modell Beltrami és Klein cégtől

Eugenio Beltrami és Felix Klein által kifejlesztett ábrázolásban a következők érvényesek:

• A hiperbolikus síkot egy nyitott körlemez modellezi.
• A hiperbolikus vonalakat inak modellezik.
• A hosszakat egy speciális távolságfüggvény határozza meg (a szögek is eltérnek az euklideszi értékektől).

Ez az ábrázolás "sörszőnyeg-geometria" néven is ismert.

Távolságfüggvény

A hiperbolikus geometria két pontja közötti távolság

Vannak A és B két pont a kör alakú lemez, úgyhogy megfelel A és B kiterjesztése akkord a kör két pontban R és S . Az A és B közötti hiperbolikus távolságot most a kettős arány alkalmazásával határozzuk meg : ${\ displaystyle (A, B, R, S)}$

${\ displaystyle d (A, B) = {\ frac {1} {2}} \ ln (A, B, R, S) = {\ frac {1} {2}} \ ln {\ frac {{\ overline {RB}} \ cdot {\ overline {SA}}} {{\ overline {RA}} \ cdot {\ overline {SB}}}}}$.

Poincaré körlemez modell

A következő vonatkozik Henri Poincaré körkörös lemezmodelljére , amely Beltramira nyúlik vissza :

• A hiperbolikus síkot egy nyitott kör alakú lemez (általában az egység kör) modellezi.
• A hiperbolikus egyeneseket az élre merőleges ívek (és átmérők ) modellezik.
• A hiperbolikus szög mérési megfelel az euklideszi szögmérés, a szög két ív határozza meg azok érintők a metszéspontja.
• A hiperbolikus hosszmérést egy speciális távolságfüggvény segítségével hajtják végre.

Távolságfüggvény

Legyen és legyen a körlemez két pontja. Összefoglalva a sík komplex síkban, így megfelelnek a pont , komplex számok , . A hiperbolikus távolság és a következő komplex számok alapján van meghatározva: ${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle A}$${\ displaystyle B}$

${\ displaystyle d (A, B) = \ kezelőnév {arcosh} \ bal (1 + {\ frac {2 \ cdot \ bal \ | ab \ jobb \ | ^ {2}} {\ bal (1- \ bal \ | a \ jobb \ | ^ {2} \ jobb) \ cdot \ bal (1- \ bal \ | b \ jobb \ | ^ {2} \ jobb)}} \ jobb)}$

Poincaré félsík modell

Henri Poincaré félsíkú modelljében, amely Beltramira nyúlik vissza:

• A hiperbolikus síkot a felső félsík (y> 0) modellezi.
• A hiperbolikus egyeneseket az x tengelyre merőleges ívek (és félegyenesek ) modellezik.
• A hiperbolikus szögmérés megfelel az euklideszi szögmérésnek, ahol a két ív közötti szöget érintésük határozza meg a metszésponton.

Távolságfüggvény

A felső félsík két pontja közötti távolság kiszámítása a következő képlettel történik:

${\ displaystyle \ operátornév {d} (\ langle x_ {1}, y_ {1} \ rangle, \ langle x_ {2}, y_ {2} \ rangle) = \ operatorname {arcosh} \ bal (1 + {\ frac {{(x_ {2} -x_ {1})} ^ {2} + {(y_ {2} -y_ {1})} ^ {2}} {2y_ {1} y_ {2}}} \ jobb) \ ,.}$

Hiperboloid modell

A hiperboloid modell, amely Poincaréig nyúlik vissza, beágyazza a hiperbolikus síkot a háromdimenziós Minkowski térbe .

Erlangen program

Abban az értelemben, Felix Klein Erlangeni program, hiperbolikus geometria a geometria

${\ displaystyle (O (n, 1), O (n) \ szorozva O (1))}$.

A Beltrami-Klein modell azt mutatja, hogy a hiperbolikus geometria a projektív geometria részeként is felfogható.

háromszög

Háromszög a hiperbolikus térben

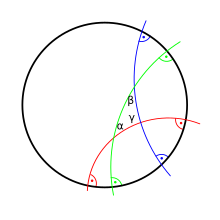
Valódi hiperbolikus geometriában a háromszög szögeinek összege mindig kisebb, mint π (180 fok; vagy két jog, ha el akarjuk kerülni a szögméretet). Nagyon nagy háromszögek esetén elkészítheti olyan kicsi, amennyit csak akar. A háromszög területét Johann Heinrich Lambert képletével számolják:

${\ displaystyle \ pi - (\ alpha + \ beta + \ gamma) = C \, \ Delta,}$

ahol α , β és γ a megfelelő szög, Δ a terület és a C állandó skálázási tényező. A C méretezési tényező a használt egységek rendszerétől függ, és alapvetően 1-re kell állítani. Ha a C tényező negatív, akkor egy (pozitív) Gauss-görbületről beszélünk . Hasonlóképpen, Thomas Harriot korábban 1603-ban meghatározta a képletet

${\ displaystyle \ Delta = R ^ {2} \, (\ alpha + \ beta + \ gamma - \ pi)}$

a gömbéval azonos sugarú körökből álló gömb felületén lévő háromszög területére. A kapcsolat itt érvényes

${\ displaystyle C = - {\ frac {1} {R ^ {2}}}}$.

Mivel a hiperbolikus geometriát igényel egy pozitív értéket a C , R kell lennie miatt

${\ displaystyle R = (- C) ^ {- {\ frac {1} {2}}}}$

képzeletbeli sugár körül járjon el .

Lásd még

• Hiperbolikus tér
• Elliptikus geometria
• Nyikolaj Lobacsevszkij
• Bolyai János
• Giovanni Girolamo Saccheri és Saccheri-Viereck

irodalom

történelem

• Jeremy Gray: A tér ötletei: euklideszi, nem euklideszi és relativisztikus . 2. kiadás. Oxford University Press, Oxford 1989, ISBN 0-19-853935-5 . 
• Marvin Jay Greenberg: euklideszi és nem euklideszi geometriák: fejlődés és történelem. WH Freeman, 1993, ISBN 0-7167-2446-4 .
• David Hilbert : A geometria alapjai . 14. kiadás. Teubner, Stuttgart / Leipzig 1999, ISBN 3-519-00237-X ( az 1903. évi kiadás online példánya [hozzáférés: 2013. június 28.]). 
• Nyikolaj I. Lobacsevszkij: Pangeometria, szerkesztette és fordította: Athanase Papadopoulos, Az európai matematika öröksége. 4. kötet, Európai Matematikai Társaság (EMS), Zürich, ISBN 978-3-03719-087-6 .

A hiperbolikus geometria a differenciálgeometria összefüggésében (geometriák a felületeken)

• Norbert A'Campo, Athanase Papadopoulos: Megjegyzések a hiperbolikus geometriához. In: Strasbourgi mester osztály a geometriáról. Európai Matematikai Társaság (EMS), Zürich, ISBN 978-3-03719-105-7, 1–182., Doi: 10.4171 / 105 . (IRMA matematika és elméleti fizika előadások, 18. kötet)
• Athanase Papadopoulos (Szerk.): Teichmüller-elmélet kézikönyve. I. köt., Európai Matematikai Társaság (EMS), Zürich 2007, ISBN 978-3-03719-029-6 , doi: 10.4171 / 029 . (IRMA matematika és elméleti fizika előadások 11)
• Athanase Papadopoulos (Szerk.): Teichmüller-elmélet kézikönyve. II. Kötet, Európai Matematikai Társaság (EMS), Zürich 2009, ISBN 978-3-03719-055-5 , doi: 10.4171 / 055 . (IRMA matematika és elméleti fizika előadások 13)
• Athanase Papadopoulos (Szerk.): Teichmüller-elmélet kézikönyve. III. Kötet, Európai Matematikai Társaság (EMS), Zürich, 2012, ISBN 978-3-03719-103-3 , doi: 10.4171 / 103 . (IRMA matematika és elméleti fizika előadások 19)

A (valós) hiperbolikus sík, mint a Hilbert-féle értelemben vett abszolút geometria modellje

• Friedrich Bachmann : A geometria felépítése a reflexió fogalmából . 2. kiegészített kiadás. Springer, Berlin / Heidelberg / New York 1973, ISBN 3-540-06136-3 , V: Hiperbolikus geometria és § 20.13: Hilbert Planes (az abszolút geometriát nagyon általánosan meghatározza, a valódi hiperbolikus geometria sajátosságait magyarázza ezen a háttéren). 
• Benno Klotzek: Euklideszi és nemeuklideszi elemi geometriák . 1. kiadás. Harri Deutsch, Frankfurt am Main 2001, ISBN 3-8171-1583-0 (az elemi itt nem egyszerűen azt jelenti : építési feladatok megoldása és a „klasszikus” nem euklideszi geometriák összehangolása). 

Egyéni bizonyíték

1. ↑ ^{a b} Klotzek (2001), 2.1
2. ↑ Susanne Müller-Philipp, Hans-Joachim Gorski: Útmutató a geometriához: oktatói állások hallgatói számára . Vieweg + Teubner Verlag, 5. kibővített kiadás, 2012, ISBN 978-3-8348-1234-6 , 71. o. ( Részlet (Google) )