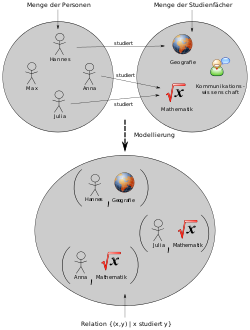
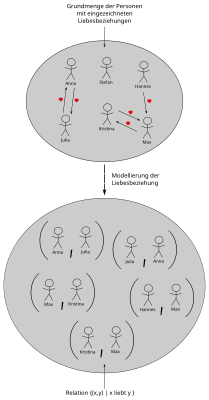
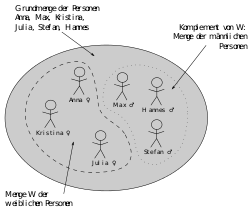
Kapcsolat (matematika)

A kapcsolat ( latin relatio "kapcsolat", "kapcsolat") általában olyan kapcsolat, amely létezhet a dolgok között. A matematika értelmében vett kapcsolatok kizárólag azok a kapcsolatok, amelyek esetében mindig egyértelmű, hogy léteznek -e vagy sem; A tárgyak nem kapcsolódhatnak egymáshoz „bizonyos mértékig”. Ez lehetővé teszi az egyszerű set- elméleti fogalom meghatározása: A kapcsolat egy sor sorok . Az egymással kapcsolatos dolgok sorokat alkotnak , amelyek elemei . ${\ displaystyle R}$${\ displaystyle n}$${\ displaystyle R}$${\ displaystyle n}$${\ displaystyle R}$

Hacsak másképp nem jelezzük, a relációt általában kétjegyű vagy bináris relációnak kell tekinteni . Az ilyen kapcsolat, akkor két elem képezi és egy rendezett pár származnak és különböző bázis szintjét , és a neve a kapcsolat heterogén vagy „kapcsolatban közötti összegek és ”. Ha az alap mennyiségek egyeznek ( ), az azt jelenti, a kapcsolat homogén vagy a „kapcsolat a vagy a tömegből .”${\ displaystyle a}$${\ displaystyle b}$ ${\ displaystyle (a, b).}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle A = B}$${\ displaystyle A}$

Fontos speciális esetekben , például egyenértékűség kapcsolatok és rendezési relációk , amelyek kapcsolatokat a szett.

Napjainkban egyes szerzők a reláció kifejezést nem feltétlenül korlátozzák, de a rendezett párokból álló osztályokat relációnak tekintik.

Definíciók

Kétszámjegyű reláció

A kétjegyű kapcsolatban (más néven bináris reláció ) között két és egy részhalmaza a Descartes-szorzat${\ displaystyle R}$${\ displaystyle A}$${\ displaystyle B}$ ${\ displaystyle A \ times B = \ {(a, b) \ mid a \ in A, b \ in B \} \ kettőspont}$

${\ displaystyle R \ subseteq A \ times B}$.

A beállított nevezzük a forrás set (angolul: set indító ) viszonyának , a készlet a kitűzött (angolul: set rendeltetési ).${\ displaystyle A}$${\ displaystyle R}$${\ displaystyle B}$

Néha azonban ez a definíció nem elég pontos, és a forrás definíciójára és a célmennyiségre hivatkozva a fenti, a gráf (ritkábban gróf ) részhalmaza, amelyet relációnak neveznek. Egy kétjegyű kapcsolatban azután meghatározzuk mint egy hármas${\ displaystyle G_ {R}}$${\ displaystyle R}$

${\ displaystyle R = (G_ {R}, A, B)}$-val .${\ displaystyle G_ {R} \ equiv \ operatornév {Graph} (R) \ subseteq A \ times B}$

A forrás és a célhalmaz ismerete különösen fontos, ha a függvényeket speciális (ún. Funkcionális) relációknak tekintjük.

A archetípusa, érvelés vagy meghatározás , vagy pre-tartomány egy adott kétjegyű kapcsolatban azt értjük, hogy a lehető legkisebb pre-tartományban, hogy a grafikon , amelynek elemeit mind megjelennek a rendezett párokat ténylegesen a bal oldali, jelekben ${\ displaystyle R}$${\ displaystyle G_ {R}}$${\ displaystyle R}$

${\ displaystyle Db (R) \ equiv {\ mathfrak {D}} (R): = \ {a \ mid \ létezik b \ kettőspont (a, b) \ a G_ {R} \} \ alállomásban A}$.

A tartomány a értékek, értékek vagy kép , vagy poszt-tartomány jelöli ebben az értelemben a legkisebb utáni tartományban egy adott egyetlen , amelynek elemei tehát mind megjelennek a párok a jobb oldali, a karakterek ${\ displaystyle G_ {R}}$${\ displaystyle R}$${\ displaystyle R}$

${\ displaystyle Wb (R) \ equiv {\ mathfrak {B}} (R): = \ {b \ mid \ létezik a \ kettőspont (a, b) \ a G_ {R} \} \ B alkategóriában}$.

Esetenként a mező (vagy csomóponthalmaz ) kifejezést használják az egyesítési halmazhoz , karakterekben

${\ displaystyle Fd (R) \ equiv {\ mathfrak {F}} (R): = Db (R) \ cup Wb (R) = \ {x \ mid \ létezik x '\ kettőspont (x, x') \ G_ {R} \ lor (x ', x) \ in R \} \ subseteq A \ cup B}$.

Ezenkívül a következő jelölések találhatók:

• Domain (angol domain ) vagy az (elvileg tetszőlegesen nagy) forráskészlethez, vagy az eredeti képkészlethez (a grafikon határozza meg) (a definíció tartománya),${\ displaystyle \ operatornév {dom} R}$
• Co-tartomány (angolul codomain , tartomány ) vagy a kitűzött vagy a kép beállítva,${\ displaystyle \ operatornév {cod} R, \ operatornév {futott} R}$
• Csomópontok halmaza ( ) a reláció mezőjéhez.${\ displaystyle \ operatornév {ver} R}$

Ha két reláció megegyezik grafikonjaikban, az egyik azt is mondja, hogy lényegében ugyanazok.
Példa: Minden reláció lényegében azonos a homogén relációval és azzal . ${\ displaystyle R = (G_ {R}, A, B)}$${\ displaystyle (G_ {R}, Db (R), Wb (R))}$ ${\ displaystyle (G_ {R}, Fd (R), Fd (R))}$

n -számjegy reláció

Általánosságban elmondható, hogy a -digit reláció a halmazok derékszögű szorzatának részhalmaza${\ displaystyle n}$ ${\ displaystyle R}$${\ displaystyle n}$${\ displaystyle A_ {1}, \ dotsc, A_ {n}}$

${\ displaystyle R \ subseteq A_ {1} \ times \ dotsb \ times A_ {n}}$-val .${\ displaystyle A_ {1} \ times \ dotsb \ times A_ {n} = \ {(a_ {1}, \ dotsc, a_ {n}) \ mid a_ {1} \ in A_ {1}, \ dotsc, a_ {n} \ in A_ {n} \} = \ texttyle \ prod A}$

Itt jelöli a véges sorozata a készletek, és a Descartes-szorzat.${\ displaystyle A = (A_ {i}) _ {i \ in \ {1, \ dot n \}}}$${\ displaystyle \ texttyle \ prod A = \ texttyle \ prod _ {i = 1} ^ {n} A_ {i}}$

A részletesebb meghatározás általánosítható a -jel kapcsolatokra is, és azután megkapjuk a -t ${\ displaystyle n}$${\ displaystyle (n + 1)}$

${\ displaystyle R = (G_ {R}, A_ {1}, \ dotsc, A_ {n}) = (G_ {R}, A)}$-val .${\ displaystyle G_ {R} \ equiv \ operatornév {Graph} (R) \ subseteq A_ {1} \ times \ dotsb \ times A_ {n} = \ texttyle \ prod A}$

A forró szállítók összegei a minimális támogatással összefüggnek a grafikonon , nevezetesen ${\ displaystyle A_ {1}, \ dotsc, A_ {i}, \ dotsc, A_ {n}}$${\ displaystyle G_ {R}}$

${\ displaystyle Tr_ {i} (R) \ equiv {\ mathfrak {T}} _ {i} (R): = \ {a_ {i} \ mid \ létezik a_ {1}, \ dotsc, a_ {i- 1}, a_ {i + 1}, \ dotsc, a_ {n} \ kettőspont (a_ {1}, \ pöttyös, a_ {i-1}, a_ {i}, a_ {i + 1}, \ pont, a_ {n}) \ itt: G_ {R} \}}$.

Az -digit reláció mezőjét a${\ displaystyle n}$

${\ displaystyle Fd (R) \ equiv {\ mathfrak {F}} (R): = \ texttyle \ bigcup \ {Tr_ {i} (R) \ mid 1 \ leq i \ leq n \} \ subseteq \ texttyle \ nagydarab A}$.

A lényegi egyenlőséget ugyanúgy határozza meg, mint a kétjegyű relációk esetében a grafikonok megfelelősége, különösen minden számjegyű reláció lényegében azonos a homogén relációval és azzal . ${\ displaystyle n}$${\ displaystyle R = (G_ {R}, A_ {1}, \ dotsc, A_ {n})}$${\ displaystyle (G_ {R}, Tr_ {1} (R), \ dotsc, Tr_ {n} (R))}$${\ displaystyle (G_ {R}, \ underbrace {Fd (R), \ dotsc, Fd (R)} _ {n {\ text {times}}})}$

Egy- és nullajegyű reláció

A halmazon belüli egy számjegyű reláció tehát egyszerűen részhalmaz , a részletes definícióban a . ${\ displaystyle A}$${\ displaystyle R \ subseteq A}$${\ displaystyle R = (G_ {R}, A)}$${\ displaystyle G_ {R} \ subseteq A}$

A nulla számjegyű relációk tehát az üres derékszögű szorzat részhalmazai, vagy , és , és részletes és . ${\ displaystyle \ texttyle \ prod _ {i = 1} ^ {0} A_ {i} = \ {\ emptyyset \}}$${\ displaystyle A ^ {0} = \ {\ emptyyset \}}$${\ displaystyle \ emptyyset}$${\ displaystyle \ {\ emptyyset \}}$${\ displaystyle (\ emptyyset, \ {\ emptyyset \})}$${\ displaystyle (\ {\ emptyyset \}, \ {\ emptyyset \})}$

Kapcsolatok valós osztályok között vagy azokon

Gyakran egy reláció hordozóterületei nem halmazok, hanem valós osztályok , azután osztályosztály -kapcsolatokról beszélünk. Esetenként el lehet kerülni az ebből adódó halmazelméleti problémákat, ha csak a megfelelő reláció grafikonját nézzük. A (minimális) hordozómennyiségek ( a kétjegyű esetmeghatározásban és értékkészletben ) valójában mennyiségek, de nem szükséges a forrásmennyiséget , a célmennyiséget,  ... ( ) eleve megadni , ha az összefüggések lényegében a azonos. Ez nem mindig lehetséges, például az egyenletesség ekvivalenciaviszonyához , lásd még: Bíboros számok §Definíció . Lényegében a kapcsolatok egyenlősége egy másik példa. ${\ displaystyle A_ {i}}$${\ displaystyle Tr_ {i} (R)}$${\ displaystyle Db (R), Wb (R)}$${\ displaystyle A, B, A_ {i}, \ dotsc}$

A két számjegyű osztályviszonyokat a forrásosztályokkal és a célosztályokkal kis elődnek nevezzük, ha az előd osztálya (archetípus szála , lásd alább) mindenki számára halmaz (azaz nem valós osztály). A relációt angol jobb-keskenynek nevezik (németül az utódról kicsi ), ha az utód minden osztályának (képszála ) sok. Abban az esetben jobb egyediség (részleges leképezések leképezések, lásd alább), egy osztály kapcsolatban mindig kicsi, hiszen egy kép értéke az egyes archetípus (pontosan vagy legfeljebb), vagyis az osztály utódainak egy sor is (vagy az üres készlet ). Minden injektív osztályleképezés kicsi és korábbi kicsi. A befogadási reláció minden osztálynál kicsi, mivel nem lehetnek valódi osztályok, hanem halmazok, és ezért halmazok is. A kifejezések elődje és utóda maguk általában használt összefüggésben rendű kapcsolatok, lásd sorrendben kapcsolatban §Predecessors és utódai . ${\ displaystyle R}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle b \ in B}$${\ displaystyle \ {a \ A \ mid aRb \}}$${\ displaystyle b}$${\ displaystyle a \ in A}$${\ displaystyle \ {b \ B \ a a rb közepén \}}$${\ displaystyle a}$${\ displaystyle \ in}$${\ displaystyle B}$${\ displaystyle b \ in B}$${\ displaystyle \ {a \ in A \ mid a \ in b \} \ subseteq b}$

Magyarázatok és jelölések

A Descartes-szorzat a két , és a készlet minden rendezett párok a és ahol bármely elem a beállított és egyet képvisel. A rendezett párban a sorrend fontos; H. különbözik ellentétben a rendezetlen pár, amely azonos a A , is írt világossá tenni, hogy van, hogy kapcsolat közötti a tárgyak (mint a ). Az üres halmaz , mint egy része a Descartes-set termék értendő kapcsolatban az úgynevezett zéró kapcsolatban , a termék teljes neve a minden vonatkozásában (más néven univerzális kapcsolatban ) (más néven ).${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle a}$${\ displaystyle b,}$${\ displaystyle a}$${\ displaystyle A}$${\ displaystyle b}$${\ displaystyle B}$${\ displaystyle (a, b)}$${\ displaystyle (b, a),}$ ${\ displaystyle \ {a, b \},}$${\ displaystyle \ {b, a \}.}$${\ displaystyle (a, b) \ in R}$${\ displaystyle a \; R \; b,}$${\ displaystyle a> b}$ ${\ displaystyle \ mathrm {O}: = \ emptyyset = \ {\}}$${\ displaystyle \ mathrm {U}}$${\ displaystyle \ nabla}$

Kapcsolatok és funkciók

• A függvény különleges, nevezetesen a bal és a jobb egyértelmű (kétjegyű) reláció, lásd alább .${\ displaystyle f \ kettőspont A \ - B}$
• A multifunkció egy baloldali teljes összefüggés .${\ displaystyle f \ colon X \ multimap Y}$${\ displaystyle f \ subseteq A \ times B}$
• A parciális függvény jobb-egyértelmű összefüggés (általában nem baloldali összesség) .${\ displaystyle f \ colon \; X \ rightharpoonup Y}$${\ displaystyle f \ subseteq A \ times B}$

Minden esetben (vagy ha a részletes meghatározást alkalmazzák). ${\ displaystyle f \ subseteq A \ times B}$${\ displaystyle G_ {f} \ subseteq A \ times B}$

A következők vonatkoznak a funkciókra és a többfunkciós funkciókra:

A részletesebb meghatározására , mert az egyértelműen meghatározott (bal összesen), akkor is lehet hagyni, és használják még egyszerűbben .${\ displaystyle f = (G_ {f}, A, B)}$${\ displaystyle A}$${\ displaystyle G_ {f}}$${\ displaystyle A}$${\ displaystyle f = (G_ {f}, B)}$

A következők vonatkoznak a funkciókra és a részfunkciókra:

For vagy is van írva (angolul: maplet ), vagy .${\ displaystyle (a, b) \ in f}$${\ displaystyle (a, b) \ in G_ {f}}$${\ displaystyle f \ kettőspont a \ mapsto b}$${\ displaystyle f (a) = b}$

Általánosságban:

1. A nulla hely relációinak (mint nulla hely nulla reláció) és (mint nulla hely teljes relációnak) jellegzetes funkciói a logikai vagy logikai állandók, és mint mindig a nulla reláció és minden reláció esetében.${\ displaystyle \ mathrm {O} = \ emptyyset}$${\ displaystyle \ mathrm {U} = \ {\ emptyyset \}}$ ${\ displaystyle {\ mathsf {rossz}}}$${\ displaystyle {\ mathsf {true}}}$
2. Az egy számjegyű kapcsolatok esete triviális.
3. Egy reláció (vagy ) egyedi módon megfelel egy igazságfüggvénynek . Ez a funkció is ismert, mint az indikátor funkció vagy karakterisztikus függvénye a részhalmaz (vagy ), ahol is helyettesíthető a .${\ displaystyle R \ subseteq A \ times B}$${\ displaystyle R = (G_ {R}, A, B)}$ ${\ displaystyle \ chi _ {R} \ kettőspont \; A \ alkalommal B \ - \ {{\ mathsf {true}}, {\ mathsf {false}} \}}$${\ displaystyle R \ subseteq A \ times B}$${\ displaystyle G_ {R} \ subseteq A \ times B}$${\ displaystyle \ {{\ mathsf {true}}, {\ mathsf {false}} \}}$${\ displaystyle \ {1,0 \}}$
4. Egy -számjegy reláció (vagy ) a jellemző függvénynek felel meg${\ displaystyle n}$${\ displaystyle R \ subseteq A_ {1} \ times \ dotsb \ times A_ {n}}$${\ displaystyle R = (G_ {R}, A_ {1}, \ dotsc, A_ {n})}$${\ displaystyle \ chi _ {R} \ kettőspont A_ {1} \ times \ dotsb \ times A_ {n} \ to \ {{\ mathsf {true}}, {\ mathsf {false}} \}.}$

A következők érvényesek:

• ${\ displaystyle n = 0 \ kettőspont \; \ chi _ {\ emptyyset} \ Leftrightarrow {\ mathsf {false}}, \ chi _ {\ {\ emptyyset \}} \ Leftrightarrow {\ mathsf {true}}}$.

${\ displaystyle n = 1 \ kettőspont \; \ chi _ {R} (a) \ Balra nyíl a \ in R}$.

${\ displaystyle n = 2 \ kettőspont \; \ chi _ {R} (a, b) \ Balosnyíl aRb \ Balos nyíl (a, b) \ in R}$.

${\ displaystyle n> 2 \ kettőspont \; \ chi _ {R} (a_ {1}, \ dotc, a_ {n}) \ Leftrightarrow (a_ {1}, \ dotsc, a_ {n}) \ in R}$.

• Egy kapcsolatban is értelmezhető, mint leképezés az a hálózati sor , az egyik, majd gyakran beszél a levelezés , és egy átmenet vonatkozásában .${\ displaystyle R \ subseteq A \ times B}$${\ displaystyle \ kappa _ {R}}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle \ kappa _ {R} \ colon A \ to {\ mathcal {P}} (B), \; a \ mapsto \ {b \ in B \ mid (a, b) \ in R \},}$${\ displaystyle B = A}$

A kapcsolatok láncolata

Az előre kötésével két kétjegyű kapcsolatok meghatározása az alábbiak szerint: ${\ displaystyle R \ subseteq A \ times B, S \ subseteq C \ times D}$

${\ displaystyle {\ begin {array} {lll} R \; \ mathbf {;} \; S \ equiv RS &: = \ {(a, d) \ mid \ létezik b \ kettőspont \; aRb \ land bSd \ } \\ & = \ {(a, d) \ in A \ times D \ mid \ létezik b \ in B \ cap C \ colon \; (a, b) \ in R \ land (b, d) \ in S \}. \ End {tömb}}}$

A fordított sorrendben történő láncolást visszaláncolásnak nevezzük :

${\ displaystyle S \ circ R \ qquad \ quad: = \ {(a, d) \ in A \ times D \ mid \ létezik b \ in B \ cap C \ colon \; (a, b) \ in R \ föld (b, d) \ in S \} = R \; \ mathbf {;} \; S}$.

Néhány szerző (W. v. O. Quine) erre használja a jelölést alternatívaként .${\ displaystyle S \ R közepén}$

A visszaláncolás sorrendje megegyezik a láncfunkciókéval (amelyek speciális relációknak tekinthetők).

A kétjegyű kapcsolatok összefűzését relatív terméknek is nevezik . Az összefűzés során az egyes derékszögű szorzatokban legegyszerűbb reláció üres reláció ( üres halmaz ) fordulhat elő, nevezetesen, amikor és a diszjunkt szimbólumokban van . ${\ displaystyle \ emptyyset}$${\ displaystyle B}$${\ displaystyle C}$ ${\ displaystyle B \ cap C = \ emptyyset}$

Példa: A „sógornő” kapcsolat az unió

• a „testvére lenni” és a „feleségének lenni” összefüggés relatív termékének és
• a „házastárs” és a „testvér” kapcsolat relatív termékének.

Fordított összefüggés

A fordított relációt (más néven fordított relációt, fordított vagy fordított relációt) egy kétjegyű relációra úgy definiáljuk, mint ${\ displaystyle R \ subseteq A \ times B}$

${\ displaystyle {\ overset {\ smallsmile} {R}} \ equiv {} ^ {\ smallsmile} {R} \ equiv R ^ {\ sim} \ equiv R ^ {- 1}: = \ {(b, a ) \ in B \ alkalommal A \ közepén (a, b) \ R \}}$.

Időnként ezt transzponált relációnak is nevezik , karakterekben .${\ displaystyle R ^ {T}}$

• 1. példa: A „leszármazottja” összefüggés fordított kapcsolata az „őse”.
• 2. példa: A „kisebb, mint” összefüggés fordított kapcsolata a „nagyobb, mint” reláció.
• 3. példa: A „szállít” reláció fordított kapcsolata a „szállítja” reláció.

Az inverz reláció (fordított) jel -relációinak általánosítása a benne található -csövek koordinátáinak permutációja , speciális ${\ displaystyle n}$${\ displaystyle n}$

• a mindössze 2 koordináta felcserélése ( transzponálás ) és
• a sorrend megfordítása ( tükrözés ),

mindkét példa ( ciklikus ) ön-inverz permutációkra .

Hagy egy permutációs (azaz egy bijektív leképezés az önmagára), és legyen egy -place kapcsolatban, akkor a kapcsolatban kapott alkalmazása után a permutációs van (az egyik megérti , mint egy család ). Tükrözés esetén ${\ displaystyle \ pi \ kettőspont \ {1,2, \ dotsc, n \} \ rightarrow \ {1,2, \ dotsc, n \}}$${\ displaystyle \ {1, \ dotsc, n \}}$${\ displaystyle R \ subseteq (A_ {i}) _ {i \ in \ {1, \ dotsc, n \}}}$${\ displaystyle n}$${\ displaystyle S: = \ {a \ circ \ pi \ a közepén \ R \}}$${\ displaystyle \ pi}$${\ displaystyle a = (a_ {i}) _ {i \ in \ {1, \ dotsc, n \}}}$

${\ displaystyle \ pi = \ sigma _ {n} = {\ begin {pmatrix} 1 & 2 & \ cdots & n \\ n & n-1 & \ cdots & 1 \ end {pmatrix}}}$

van . ${\ displaystyle S = \ {(a_ {n}, \ dotc, a_ {1}) \ mid (a_ {1}, \ dotc, a_ {n}) \ in R \}}$

Kép és archetípus

Egy kétjegyű képest , a kép egy sor vagy osztály a set vagy osztály ${\ displaystyle R \ subseteq A \ times B}$${\ displaystyle X}$

${\ displaystyle R ^ {\ to} (X) \ equiv R \ langle X \ rangle: = \ {y \ mid \ létezik x \ X \ kettőspontban \; (x, y) \ R \}}$.

A archetípusa egy sor vagy osztály a set vagy osztály ${\ displaystyle Y}$

${\ displaystyle R ^ {\ leftarrow} (Y) \ equiv {\ overset {\ smallsmile} {R}} \ langle Y \ rangle \ equiv {} ^ {\ smallsmile} {R} \ langle Y \ rangle \ equiv R ^ {\ sim} \ langle Y \ rangle \ equiv R ^ {- 1} \ langle Y \ rangle = \ {x \ mid \ létezik y \ Y \ kettőspontban \; (x, y) \ R \}}$.

Időnként a (sic!) Megnevezést is erre találják , gyakran szögletes zárójelekkel, mint jelöléssel. A levelezés egy a kép szál olyan összeg (Singleton) , a jelölést , amit részben szintén használja a konzol jelölést használja, i. H. ; szimmetrikus összefüggések esetén d. H. (esetleg részleges) egyenértékűségi vagy kompatibilitási összefüggések a jelölések, és egyenértékűségi vagy kompatibilitási vagy toleranciaosztályokról beszélnek.${\ displaystyle R {\ grave {}} {\ grave {}} Y}$${\ displaystyle R [Y]}$${\ displaystyle \ {a \}}$${\ displaystyle \ kappa _ {R} (a) = R \ langle \ {a \} \ rangle}$${\ displaystyle R [a]}$${\ displaystyle [a] _ {R} = R \ langle \ {a \} \ rangle = R ^ {- 1} \ langle \ {a \} \ rangle}$

Korlátozás

A kapcsolatok különböző módon korlátozhatók a hordozóhalmazok részhalmazaira, további részletekért lásd: A reláció korlátozása .

Kiegészítő reláció

A fix elő- és utótartományú kétjegyű relációk esetén a kiegészítő relációt a${\ displaystyle R \ subseteq A \ times B}$${\ displaystyle A, B}$

${\ displaystyle {\ overline {R}} \ equiv {} ^ {-} R = (A \ x B) \ setminus R = \ {(x, y) \ in A \ times B \ mid (x, y) \ nem \ R \}}$,

analóg a számjegy relációkhoz a rögzített támogatási területeken . A valós számok esetében például az -hoz való kiegészítő viszony . ${\ displaystyle n}$${\ displaystyle R \ subseteq A_ {1} \ times \ dotsb \ times A_ {n}}$${\ displaystyle A = (A_ {1}, \ dotsc, A_ {n})}$${\ displaystyle \ mathbb {R}}$${\ displaystyle \ leq}$${\ displaystyle>}$

Ha a komplex jelölést használjuk, akkor az ${\ displaystyle R = (G_ {R}, A, B)}$

${\ displaystyle {\ overline {R}} \ equiv {} ^ {-} R = ((A \ x B) \ setminus G_ {R}, A, B)}$,

ahol már nincsenek külső kiegészítések, hanem a kapcsolat összetevői; analóg a számjegy relációkhoz ebben a jelölésben. ${\ displaystyle A, B}$${\ displaystyle n}$

Mint minden halmaz esetében, a kiegészítés a kapcsolatokra is bevonható:

${\ displaystyle {\ overline {\ overline {R}}} = R}$.

Homogén kapcsolatok

Ha igen , akkor az összefüggést homogénnek nevezzük . Egyes szerzők meghatározzák általános összefüggést már homogén kapcsolatban, mint általános összefüggést mindig figyelembe lehet venni, mint egy homogén korlátozása: . ${\ displaystyle A = B}$${\ displaystyle R \ subseteq A \ times A}$${\ displaystyle R \ subseteq A \ times B}$${\ displaystyle R \ subseteq (A \ cup B) \ times (A \ cup B)}$

Különleges homogén kapcsolatok és műveletek a homogén kapcsolatokon

Egy halmaz különleges homogén relációja az egyenlőség- vagy azonosságviszony vagy az átló${\ displaystyle A}$

${\ displaystyle \ mathrm {I} _ {A}: = \ {(a, b) \ in A \ times A \ mid a = b \} = \ {(a, a) \ mid a \ in A \} .}$

Az átló alternatív jelölései a vagy ; ha már ismert, akkor egyszerűen csak , vagy .${\ displaystyle \ Delta _ {A}}$${\ displaystyle \ mathrm {D} _ {A}}$${\ displaystyle A}$${\ displaystyle \ mathrm {I}}$${\ displaystyle \ Delta}$${\ displaystyle \ mathrm {D}}$

Egy másik különleges homogén reláció a minden reláció vagy univerzális reláció

${\ displaystyle \ mathrm {U} _ {A} = A \ alkalommal A}$(más néven Nabla , mint ).${\ displaystyle \ nabla _ {A}}$

Ha már ismert, az index itt is elmarad, mint az identitás reláció esetében.${\ displaystyle A}$

Az összes reláció szerepet játszik a gráfelméletben (lásd alább). Példa a felhasználásra a következő mondat:

Van egy irányított gráfban , sok a sarkok és a (társított) kapcsolatát az élek, ez ezután pontosan Coherent (erős) , amikor a visszaható tranzitív lezárása az Egyetemes kapcsolatban.${\ displaystyle G = (E, K)}$${\ displaystyle E}$${\ displaystyle K \ subseteq E \ times E}$${\ displaystyle G}$${\ displaystyle K}$

A homogén kétjegyű reláció fordított relációjának (fordított relációja) kialakulása ismét homogén kétjegyű relációt (közelséget) biztosít, két végrehajtás ismét a kiinduló relációt (involutivitást) eredményezi. Bármely (szintén nem homogén) reláció kapcsolata azzal a relációval, amelyre átalakítják, szimmetrikus és reflexív, azaz ekvivalencia reláció, de általában nem azonos az identitás relációval.

Abban az esetben, homogén kapcsolatban , a összefűzése is homogén kapcsolatban, úgy, hogy a homogén kapcsolatok formának egy monoid a multiplikatív kapcsolatban , és a semleges elem . Így, és az általános hatáskörét , hogy kell meghatározni, amely az. ezért a halmaz egy relációjának is nevezik . ${\ displaystyle R \ subseteq A \ times A}$${\ displaystyle R \ circ R}$${\ displaystyle A}$ ${\ displaystyle \ circ}$ ${\ displaystyle \ mathrm {I} _ {A}}$${\ displaystyle R ^ {2}: = R \ circ R}$ ${\ displaystyle R ^ {n}: = R \ circ R ^ {n-1}}$${\ displaystyle n \ in \ mathbb {N}}$${\ displaystyle R ^ {0}: = \ mathrm {I} _ {A}}$${\ displaystyle \ mathrm {I} _ {A}}$${\ displaystyle A}$

A jelölés kiterjesztése helyett a fordított reláció, az egyik negatív hatványokkal jelöli a hatáskörét:${\ displaystyle R ^ {- 1}}$${\ displaystyle {\ overset {\ smallsmile} {R}}}$

${\ displaystyle R ^ {- n}: = {\ overset {\ smallsmile} {R}} ^ {n} = {\ overset {\ smallsmile} {R ^ {n}}}}$.

Bármilyen egész szám megengedett kitevőként. ${\ displaystyle n \ in \ mathbb {Z}}$

Ezenkívül minden monoidnak homogén kapcsolata van az üres relációval ( nulla reláció )

${\ displaystyle \ mathrm {O} = \ emptyyset}$

egy másik nedvszívó elem .

A kapcsolatok a különböző hatalmak egyesülésével jönnek létre

${\ displaystyle R ^ {*}: = \ texttyle \ bigcup _ {n \ in {\ mathbb {N} _ {0}}} R ^ {n}}$és . ${\ displaystyle R ^ {+}: = \ texttyle \ bigcup _ {n \ in {\ mathbb {N}}} R ^ {n}}$

Algebrai szerkezetek

Együttesen a két számjegyű kapcsolatok egy sor alkot egy kapcsolatban algebra${\ displaystyle A}$

${\ displaystyle {\ mathfrak {Re}} (A) = (2 ^ {U_ {A}}, \ cap, \ cup, {} ^ {-}, \ mathrm {O}, U_ {A}, \ circ , \ mathrm {I} _ {A}, {} ^ {\ smallsmile})}$

A jelölések használata .${\ displaystyle U_ {A} = A ^ {2} = A \ times A, \; \; 2 ^ {U_ {A}} = 2 ^ {A ^ {2}} = {\ mathcal {P}} ( A \ alkalommal A)}$

A korlátozásokkal együtt a homogén kapcsolatok egy ( heterogén ) Peirce -algebrát alkotnak .

Homogén több számjegyű kapcsolatok

A homogén több számjegyű kapcsolatok (a grafikonjukkal) részhalmazai . Szilárd esetén az összes relációt (is ) és az azonossági viszonyt (átló) (is ) a ${\ displaystyle A ^ {n}}$${\ displaystyle n}$${\ displaystyle \ mathrm {U} _ {A}}$${\ displaystyle \ nabla _ {A}}$${\ displaystyle \ mathrm {I} _ {A}}$${\ displaystyle \ mathrm {D} _ {A}, \ Delta _ {A}}$

${\ displaystyle \ mathrm {U} _ {A} = A ^ {n}, \; \; \ mathrm {I} _ {A} = \ {(a_ {i}) _ {i \ in {1, \ pötty, n \}} \ A ^ {n} \ a a közepén {1} = a_ {2} = \ pöttyök = a_ {n} \}}$.

Különösen fontos itt a permutációk alkalmazása a -csonkjaikra, amelyeket a konverziók kialakulásának általánosításaként írnak le , mivel így mindig az ember a (közelség) részhalmazain belül marad . M. a. W. Ezek a műveletek bijektív leképezések . A kétszámjegyű relációkból ismert egyéb kifejezések, mint például a reflexivitás és a szimmetria stb., Kanonikusan (természetesen) kiterjeszthetők minden többjegyű relációra. ${\ displaystyle n}$${\ displaystyle A ^ {n}}$${\ displaystyle {\ mathcal {P}} (A ^ {n}) = 2 ^ {A ^ {n}}}$

Gráfelmélet és általánosítások

A gráfelmélet a velük összefüggő halmazokat írja le, bizonyos általánosításokkal együtt, egy általános általános kifejezés, a gráf alatt . A gráfelméletben figyelembe vett esetek (hacsak másként nem jelezzük) általában végesek.

1. A relációs szerkezetet, amely egy halmazból és egy rajta lévő relációból áll, irányított (szintén orientált ) gráfnak nevezzük . az úgynevezett set of csomópontjainak a gráf, annak elemei nevezzük csomópontok . nevezzük egy részhalmaza az élek halmaza , annak elemei (rendezett párokat ) nevezzük irányított (azaz, orientált ) szélei . ${\ displaystyle G}$${\ displaystyle M}$${\ displaystyle R}$ ${\ displaystyle G = (M, R)}$${\ displaystyle M = V (G)}$${\ displaystyle E (G) = R}$${\ displaystyle M \ times M}$${\ displaystyle M}$

2. Szimmetrikus gráfok , i. H. Beállítja a szimmetrikus kapcsolatban egyenértékűek irányítatlan gráf , amelynek pereme készlet áll (irányítatlan) élei, azaz a (rendezetlen) készletek az (itt egyenértékű ). ${\ displaystyle G = (M, R)}$${\ displaystyle M}$${\ displaystyle R}$ ${\ displaystyle G ': = (M, \ {\ {a, b \} \ mid a \; R \; b \})}$${\ displaystyle E (G ')}$${\ displaystyle \ {a, b \}}$${\ displaystyle a \ R \ b}$${\ displaystyle b \ R \ a}$

3. További általánosítások az úgynevezett irányított gráfokra vonatkoznak, amelyeknek több éle van kombinálva , és amelyek mindegyik élének természetes száma sokszoros. Az élek ilyen grafikonokat képviseli multihalmaz : a térkép egy sor és egy térképet , mely kijelöli a pozitív számot hívott egy színt minden egyes csomóponthoz . A színes csomópontokkal és / vagy élekkel rendelkező grafikonok hasonlóak .${\ displaystyle {\ boldsymbol {M}}}$${\ displaystyle {\ boldsymbol {M}} = (M, f)}$${\ displaystyle M = supp ({\ boldsymbol {M}})}$${\ displaystyle f \ colon \; M \ to \ mathbb {N}}$${\ displaystyle v \ in M}$${\ displaystyle f (v)}$

4. Súlyozott csomópontokról és / vagy élekről: Súlyokról beszélünk színek helyett, ha a leképezés valós értékű. A Node súlyozott ez megfelel egy fuzzy halmaz , ahol az egy valós értékű multihalmaz . Ugyanez vonatkozik a súlyozott élekre is. Az orientált gráfok esetében ez különösen azt jelenti, hogy az élek halmaza (reláció, azaz rendezett csomópont-párok halmaza) többhalmazos vagy fuzzy halmaz lesz a relációfogalom kiterjesztésében. ${\ displaystyle f}$${\ displaystyle f \ colon \; M \ - [0,1]}$ ${\ displaystyle {\ boldsymbol {M}} = (M, f)}$${\ displaystyle f \ colon \; M \ to R ^ {+}}$${\ displaystyle {\ boldsymbol {M}} = (M, f)}$

Példák

• 

  Minden lehetséges rendezett párok együtt és , valamint a kapcsolat meghatározott közötti és${\ displaystyle (u, v)}$${\ displaystyle u \ itt: A: = \ {a, b, c \}}$${\ displaystyle v \ in B: = \ {x, y, z \}}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle R.}$

• 

  Példa kapcsolatra „Egy x személy az y tantárgyat tanulja”.

• 

  Példa az „x személy szereti y embert” összefüggésre. Ezt a kétjegyű relációt rendezett párok halmazával modellezik.

• 

  Az „egy személy x nő” egy számjegyű relációt az alaphalmaz részhalmazaként modellezik.

• 

  Az „x személy személy megtanulja az y tantárgyat a z tanárral” háromjegyű relációt 3 soros halmaz segítségével valósítják meg.

A kétjegyű relációk tulajdonságai

Általános kapcsolatok

A következő összefüggések fontosak a funkciók szempontjából (speciális kapcsolatokként ábrázolva). Általában itt az eset két különböző mennyisége közötti kapcsolat is lehetséges. ${\ displaystyle R \ subseteq A \ times B}$${\ displaystyle A, B,}$${\ displaystyle A = B}$

Az összefüggést ún ${\ displaystyle R}$	ha és csak akkor (predikátum logika)	vagy ezzel egyenértékű (mennyiségi jelölés)	és az azt jelenti:
teljes bal vagy végleges (többfunkciós)	${\ displaystyle \ forall a \ in A \; \ létezik b \ itt: {B} \ kettőspont \; (a, b) \ R}$	${\ displaystyle \ mathrm {I} _ {A} \ subseteq R ^ {- 1} \ circ R}$	Minden elemnek legalább egy partnere van${\ displaystyle A}$${\ displaystyle B.}$
jobb totális vagy szuverzív	${\ displaystyle \ forall b \ in B \; \ létezik a \ A \ kettőspontban \; (a, b) \ R}$	${\ displaystyle \ mathrm {I} _ {B} \ subseteq R \ circ R ^ {- 1}}$	Minden elemnek legalább egy partnere van${\ displaystyle B}$${\ displaystyle A.}$
egyértelmű vagy injektív	${\ displaystyle {\ begin {aligned} & \ forall b \ in B \; \ forall a, c \ in A \ colon \\ & (a, b) \ in R \, \ land \, (c, b) \ in R \; \ Jobbra nyíl \; a = c \ end {igazítva}}}$	${\ displaystyle R ^ {- 1} \ circ R \ subseteq \ mathrm {I} _ {A}}$	Minden elem legfeljebb egy partnerrel rendelkezik${\ displaystyle B}$${\ displaystyle A.}$
(jogilag) egyértelmű (részfunkció)	${\ displaystyle {\ begin {aligned} & \ forall a \ in A \; \ forall b, d \ in B \ colon \\ & (a, b) \ in R \, \ land \, (a, d) \ in R \; \ Jobbra nyíl \; b = d \ end {igazítva}}}$	${\ displaystyle R \ circ R ^ {- 1} \ subseteq \ mathrm {I} _ {B}}$	Minden elem legfeljebb egy partnerrel rendelkezik${\ displaystyle A}$${\ displaystyle B.}$

Az összefüggést ún ${\ displaystyle R}$	ha és csak akkor (predikátum logika)	vagy ezzel egyenértékű (mennyiségi jelölés)	és az azt jelenti:
bitotális	${\ displaystyle {\ begin {aligned} & (\ forall a \ in A \; \ létezik b \ B \ colon \; (a, b) \ in R) \\\ land \; & (\ forall b \ a B \; \ -ben létezik a \ az A \ kettőspontban \; (a, b) \ az R -ben) \ vége {igazítva}}}$	${\ displaystyle {\ begin {aligned} & \ mathrm {I} _ {A} \ subseteq R ^ {- 1} \ circ R \\\ land \; & \ mathrm {I} _ {B} \ subseteq R \ kör R ^ {- 1} \ vége {igazítva}}}$	Minden elemnek legalább egy partnere van, és fordítva. ${\ displaystyle A}$${\ displaystyle B}$
félreérthetetlen	${\ displaystyle {\ begin {aligned} & \ forall b, d \ in B \; \ forall a, c \ in A \ colon \\ & (a, b) \ in R \, \ land \, (c, b) \ R \; \ Jobbra mutató nyila \; a = c, \\ & (a, b) \ R \, \ land \, (a, d) \ in R \; \ Rightarrow \; b = d \ vége {igazítva}}}$	${\ displaystyle {\ begin {aligned} & R ^ {- 1} \ circ R \ subseteq \ mathrm {I} _ {A} \\\ land \; & R \ circ R ^ {- 1} \ subseteq \ mathrm {I} _ {B} \ end {aligned}}}$	Minden elemnek legfeljebb egy partnere van, és fordítva. ${\ displaystyle B}$${\ displaystyle A}$
bijektív	${\ displaystyle \ forall b \ in B \; \ létezik! a \ A \ kettőspontban \; (a, b) \ R}$	${\ displaystyle {\ begin {aligned} & \ mathrm {I} _ {B} \ subseteq R \ circ R ^ {- 1} \\\ land \; & R ^ {- 1} \ circ R \ subseteq \ mathrm {I} _ {A} \ end {aligned}}}$	Minden elemnek pontosan egy partnere van${\ displaystyle B}$${\ displaystyle A.}$
Ábra vagy funkció	${\ displaystyle \ forall a \ in A \; \ létezik! b \ B \ kettőspontban \; (a, b) \ R}$	${\ displaystyle {\ begin {aligned} & \ mathrm {I} _ {A} \ subseteq R ^ {- 1} \ circ R \\\ land \; & R \ circ R ^ {- 1} \ subseteq \ mathrm {I} _ {B} \ end {aligned}}}$	Minden elemnek pontosan egy partnere van${\ displaystyle A}$${\ displaystyle B.}$

Funkciók

A kapcsolatok funkcionális tulajdonságainak áttekintése

A reláció tehát akkor és csak akkor (teljes) függvény, ha a totális és a jobb egyértelmű. Ez azt jelenti, hogy A -ban minden elemnek pontosan egy partnere van B -ben. A szujektív, injektív és bijective tulajdonságokat általában függvényekhez használják, és bizonyos további tulajdonságokat határoznak meg. Például egy függvény (és bármely reláció) akkor és csak akkor bijektív, ha szujektív és injektív, azaz ha fordított kapcsolata függvény. ${\ displaystyle R}$${\ displaystyle R ^ {- 1}}$

Az összefüggést ún ${\ displaystyle R}$	pontosan mikor ő a	vagy egyenértékű (mennyiség jelölés)	és az azt jelenti:
Szívás	szürjektív funkció	${\ displaystyle {\ begin {aligned} & \ mathrm {I} _ {A} \ subseteq R ^ {- 1} \ circ R \\\ land \; & R \ circ R ^ {- 1} = \ mathrm { I} _ {B} \ vége {igazítva}}}$	Minden elemből pontosan egy partner van, és minden elemből legalább egy partner van${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle B}$${\ displaystyle A.}$
injekció	injektív funkció	${\ displaystyle {\ begin {aligned} & \ mathrm {I} _ {A} = R ^ {- 1} \ circ R \\\ land \; & R \ circ R ^ {- 1} \ subseteq \ mathrm { I} _ {B} \ vége {igazítva}}}$	Minden elemből pontosan egy partner van, és minden elemből legfeljebb egy partner van${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle B}$${\ displaystyle A.}$
Bijection	bijektív funkció	${\ displaystyle {\ begin {aligned} & \ mathrm {I} _ {A} = R ^ {- 1} \ circ R \\\ land \; & R \ circ R ^ {- 1} = \ mathrm {I } _ {B} \ vége {igazítva}}}$	Minden elemnek pontosan egy partnere van, és fordítva. ${\ displaystyle A}$${\ displaystyle B}$

Fordított függvény

Térképezést vagy függvényt is hívnak

• visszafordíthatóan egyértelmű vagy visszafordítható, ha bijektív .

Egy függvény relációként mindig reverzibilis, de függvényként pontosan akkor reverzibilis, ha a fordított relációja is függvény, tehát amikor van egy fordított függvénye .

Homogén kapcsolatok

A következő táblázatokban megadott példák a valós számok normál elrendezésére vonatkoznak, amikor a „=” egyenlőjelet, a kisebb, mint „<” jelet és a kisebb vagy egyenlő jelet „≤” használják.

Az összefüggést ún ${\ displaystyle R}$	ha és csak akkor (predikátum logika)	vagy ezzel egyenértékű (mennyiségi jelölés)	és az azt jelenti:
jobb összehasonlító vagy harmadik egyenlő	${\ displaystyle {\ begin {aligned} & \ forall a, b, c \ in A \ colon \\ & (a, c) \ in R \, \ land \, (b, c) \ in R \\ & \ Jobbra mutató nyila \; (a, b) \ R \ végén {igazítva}}}$	${\ displaystyle R ^ {- 1} \ circ R \ subseteq R}$	Ha két elem ugyanahhoz a harmadik elemhez kapcsolódik, akkor egymáshoz is kapcsolódnak. Például, és mindig érvényes${\ displaystyle a = c}$${\ displaystyle b = c}$${\ displaystyle a = b.}$
bal összehasonlító vagy euklideszi	${\ displaystyle {\ begin {aligned} & \ forall a, b, c \ in A \ colon \\ & (a, b) \ in R \, \ land \, (a, c) \ in R \\ & \ Jobbra mutató nyila \; (b, c) \ R \ végén {igazítva}}}$	${\ displaystyle R \ circ R ^ {- 1} \ subseteq R}$	Ha egy első elem kapcsolódik egy második és egy harmadik elemhez, akkor ezek is kapcsolatban állnak egymással. Például, és mindig ugyanaz${\ displaystyle a = b}$${\ displaystyle a = c}$${\ displaystyle b = c.}$
tranzitív	${\ displaystyle {\ begin {aligned} & \ forall a, b, c \ in A \ colon \\ & (a, b) \ in R \, \ land \, (b, c) \ in R \\ & \ Jobbra mutató nyila \; (a, c) \ R \ végén {igazítva}}}$	${\ displaystyle R \ circ R \ subseteq R}$	Ha az első elem egy második elemhez kapcsolódik, ez pedig egy harmadik elemhez, akkor az első elem szintén a harmadik elemhez kapcsolódik. Például ebből következik és mindig${\ displaystyle a <b}$${\ displaystyle b <c}$${\ displaystyle a <c.}$
tárgyatlan	${\ displaystyle {\ begin {aligned} & \ forall a, b, c \ in A \ colon \\ & (a, b) \ in R \, \ land \, (b, c) \ in R \\ & \ Jobbra mutató nyila \; (a, c) \ notin R \\\ end {aligned}}}$	${\ displaystyle (R \ circ R) \ cap R = \ emptyyset}$	Ha két elem kapcsolódik, a második pedig egy harmadik elemhez, akkor az első elem nem kapcsolódik a harmadik elemhez. Például minden természetes szám a (azonnali) elődje a és a (azonnali) elődje , de nem az (azonnali) elődje${\ displaystyle n}$${\ displaystyle n + 1}$${\ displaystyle n + 1}$${\ displaystyle n + 2,}$${\ displaystyle n}$${\ displaystyle n + 2.}$

A nem- tranzitivitás (azaz az összefüggés nem tranzitív), az intransitivitás és a negatív tranzitivitás különböznek egymástól.

Az összefüggést ún ${\ displaystyle R}$	ha és csak akkor (predikátum logika)	vagy ezzel egyenértékű (mennyiségi jelölés)	és az azt jelenti:
visszaható	${\ displaystyle \ forall a \ in A \ kettőspont (a, a) \ R}$	${\ displaystyle \ mathrm {I} \ subseteq R}$	Minden elem önmagához kapcsolódik, pl. B. mindig${\ displaystyle a \ leq a.}$
		${\ displaystyle \ mathrm {I} \ cap R = \ mathrm {I}}$
nem reflexív	${\ displaystyle \ forall a \ in A \ kettőspont (a, a) \ notin R}$	${\ displaystyle \ mathrm {I} \ cap R = \ emptyyset}$	Egyetlen elem sem kapcsolódik önmagához, pl. B. egyikre sem vonatkozik${\ displaystyle a <a}$${\ displaystyle a.}$

Az összefüggést ún ${\ displaystyle R}$	ha és csak akkor (predikátum logika)	vagy ezzel egyenértékű (mennyiségi jelölés)	és az azt jelenti:
szimmetrikus	${\ displaystyle {\ begin {aligned} & \ forall a, b \ in A \ colon \\ & (a, b) \ in R \; \ Rightarrow \; (b, a) \ in R \ end {aligned} }}$	${\ displaystyle R ^ {- 1} \ subseteq R}$	A reláció irányítatlan, pl. B. mindig ebből következik (és fordítva) ${\ displaystyle a = b}$${\ displaystyle b = a}$
		${\ displaystyle R ^ {- 1} = R}$
antiszimmetrikus vagy identitive	${\ displaystyle {\ begin {aligned} & \ forall a, b \ in A \ colon \\ & (a, b) \ in R \, \ land \, (b, a) \ in R \\ & \ Rightarrow \; a = b \ end {igazítva}}}$	${\ displaystyle R ^ {- 1} \ cap R \ subseteq \ mathrm {I}}$	Nincs két különböző elem, amelyek mindkét irányban összefüggnek, pl. B. következik és mindig${\ displaystyle a \ leq b}$${\ displaystyle b \ leq a}$${\ displaystyle a = b.}$
aszimmetrikus	${\ displaystyle {\ begin {aligned} & \ forall a, b \ in A \ colon \\ & (a, b) \ in R \; \ Rightarrow \; (b, a) \ notin R \ end {aligned} }}$	${\ displaystyle R ^ {- 1} \ cap R = \ emptyyset}$	Nincs két olyan elem, amely mindkét irányban összefügg, pl. B. ebből mindig az következik , hogy nem állja meg a helyét. ${\ displaystyle a <b}$${\ displaystyle b <a}$

Az összefüggést ún ${\ displaystyle R}$	ha és csak akkor (predikátum logika)	vagy ezzel egyenértékű (mennyiségi jelölés)	és az azt jelenti:
teljes mértékben vagy teljesen	${\ displaystyle {\ begin {aligned} & \ forall a, b \ in A \ colon \\ & (a, b) \ in R \, \ lor \, (b, a) \ in R \ end {aligned} }}$	${\ displaystyle R ^ {- 1} \ cup R = A \ times A}$	Minden két elem összefügg, pl. B. ha mindig vagy érvényes. ${\ displaystyle a \ leq b}$${\ displaystyle b \ leq a}$
konnex vagy csatlakoztatva	${\ displaystyle {\ begin {aligned} & \ forall a, b \ in A \ kettőspont \\ & a \ neq b \\ & \ Rightarrow \; (a, b) \ in R \, \ lor \, (b , a) \ az R \ végén {igazítva}}}$	${\ displaystyle R ^ {- 1} \ cup R \ cup \ mathrm {I} = A \ alkalommal A}$	Két különböző elem kapcsolódik egymáshoz, pl. B. ha mindig vagy akkor is, ha mindig vagy érvényes. ${\ displaystyle a = b,}$ ${\ displaystyle a <b}$${\ displaystyle b <a,}$${\ displaystyle a \ leq b}$${\ displaystyle b \ leq a}$
trichotóma	${\ displaystyle {\ begin {aligned} & \ forall a, b \ in A \ colon \\ & ((a, b) \ in R \ Rightarrow (b, a) \ notin R) \, \ land \\ & (a \ neq b \\ & \ Rightarrow \; (a, b) \ in R \, \ lor \, (b, a) \ in R) \ end {aligned}}}$	${\ displaystyle {\ begin {aligned} R ^ {- 1} \ cup R \ cup \ mathrm {I} & = A \ times A \\\ land \; R ^ {- 1} \ cap R & = \ emptyyset \ end {igazítva}}}$	Minden két különböző elem mindig pontosan egy módon kapcsolódik egymáshoz, pl. B. amikor vagy vagy mindig igaz. ${\ displaystyle a <b}$${\ displaystyle b <a}$

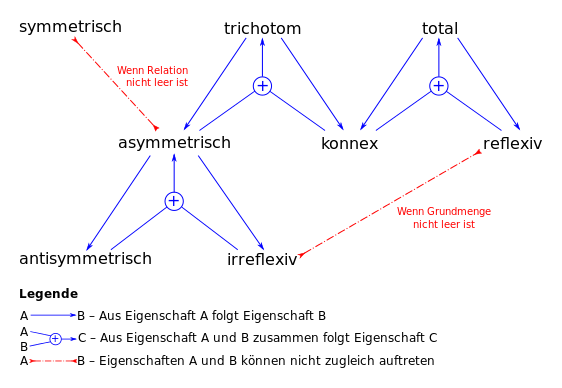
A tulajdonságok között a következő összefüggések érvényesek:

A reláció és a kiegészítő tulajdonságai között a következő összefüggések vannak: ${\ displaystyle R}$${\ displaystyle {\ overline {R}}}$

• ${\ displaystyle R}$reflexív jelentése irreflexive (és fordítva).${\ displaystyle \ iff}$ ${\ displaystyle {\ overline {R}}}$
• ${\ displaystyle R}$szimmetrikus , szimmetrikus.${\ displaystyle \ iff}$ ${\ displaystyle {\ overline {R}}}$
• ${\ displaystyle R}$az antiszimmetrikus a connectx (és fordítva).${\ displaystyle \ iff}$ ${\ displaystyle {\ overline {R}}}$
• ${\ displaystyle R}$a teljes aszimmetrikus (és fordítva).${\ displaystyle \ iff}$ ${\ displaystyle {\ overline {R}}}$

Kapcsolatok osztályai

A kapcsolatok egyéb fontos osztályai és tulajdonságaik:

• Kvázi sorrend vagy előrendelés: tranzitív és reflexív
• Kompatibilitási relációvagy toleranciaviszony : kompatibilis (reflexív és szimmetrikus) (angolul: véges esetben függőségi relációban , transzfinit esetben tolerancia relációban ).
• Ekvivalencia reláció : tranzitív, reflexív és szimmetrikus
• Részleges sorrend / részleges sorrend , részleges sorrend vagy sorrend: tranzitív, reflexív és antiszimmetrikus.
• Teljes sorrend / teljes sorrend vagy lineáris sorrend: tranzitív, reflexív, antiszimmetrikus és teljes
• Jól rendezett : lineáris sorrend, amelyben A, legkisebb elem minden egyes nem üres részhalmazavan
• Szigorú sorrend vagy szigorú részleges sorrend / részleges sorrend: tranzitív, reflexív és antiszimmetrikus (azaz aszimmetrikus)
• Szigorú teljes sorrend / teljes sorrend vagy lineáris szigorú sorrend: tranzitív, nem reflexív, antiszimmetrikus és összekötő

Kapcsolat jel

Az elemi matematikában három alapvető összehasonlító összefüggés létezik:

1. ${\ displaystyle x <y}$ (Példa: "2 kevesebb, mint 3")${\ displaystyle 2 <3,}$
2. ${\ displaystyle x = y}$ (Példa: "3 egyenlő 3")${\ displaystyle 3 = 3,}$
3. ${\ displaystyle x> y}$ (Példa: "3 nagyobb, mint 2")${\ displaystyle 3> 2,}$

-val . ${\ displaystyle x, y \ in \ mathbb {R}}$

Két valós számnak mindig pontosan egy ilyen kapcsolata van egymással. Ezekkel a relációs szimbólumokkal mások is kialakíthatók. A következők érvényesek:

• ${\ displaystyle x \ leq y}$, ha vagy (például: "4 nem nagyobb, mint 5")${\ displaystyle x <y}$${\ displaystyle x = y}$ ${\ displaystyle 4 \ leq 5,}$
• ${\ displaystyle x \ geq y}$, ha vagy (például: "5 nem kevesebb, mint 5")${\ displaystyle x> y}$${\ displaystyle x = y}$ ${\ displaystyle 5 \ geq 5,}$
• ${\ displaystyle x \ neq y}$, ha vagy (például: "4 nem egyenlő 5 -tel")${\ displaystyle x <y}$${\ displaystyle x> y}$ ${\ displaystyle 4 \ neq 5,}$

mindenkinek . ${\ displaystyle x, y \ in \ mathbb {R}}$

A fenti sorrendviszonyok nem léteznek komplex számok esetén .

A matematikusok a ≤ jelet is használják az absztrakt sorrendi kapcsolatokhoz (és ≥ a kapcsolódó fordított relációhoz), míg a „<” nem rendi reláció a matematikai definíció értelmében.

Az egyenértékűségi relációknál a „szimmetrikus” szimbólumok, például ≈, ~, ≡ előnyben részesülnek.

Kategóriaelmélet

Minden fél-gyűrű nulla elemet , és egy elem , a következő egy kategória : ${\ displaystyle (H, +, \ cdot)}$${\ displaystyle 0}$${\ displaystyle 1}$${\ displaystyle {\ mathcal {C}}}$

• ${\ displaystyle \ mathrm {Ob} ({\ mathcal {C}}) = \ mathrm {Ob} (\ mathbf {Set})}$.
• A morfizmus függvény .${\ displaystyle f \ in \ mathrm {Hom} _ {\ mathcal {C}} (X, Y)}$${\ displaystyle f \ colon X \ x Y \ H}$
• Az alábbiak az objektumokra vonatkoznak${\ displaystyle X}$

  ${\ displaystyle \ mathrm {id} _ {X} (x, x '): = {\ begin {case} 1 & x = x' \\ 0 & {\ text {egyébként}} \ end {case}}}$.

Ez azonos a Kronecker-delta : .${\ displaystyle \ mathrm {id} _ {X} (x, x ') = \ delta _ {xx'}}$

• Az alábbiak tárgyakra és morfizmusokra vonatkoznak${\ displaystyle X, Y, Z}$${\ displaystyle f \ in \ mathrm {Hom} _ {\ mathcal {C}} (Y, Z), \ g \ in \ mathrm {Hom} _ {\ mathcal {C}} (X, Y)}$

  ${\ displaystyle (f \ circ g) (x, z): = \ sum _ {y \ in Y} g (x, y) \ cdot f (y, z)}$.

A morfizmusok halmazindexelt mátrixok, és összetételük a mátrixszaporításhoz hasonlóan történik , megfelel az egységmátrixnak . ${\ displaystyle \ mathrm {id} _ {x}}$ ${\ displaystyle E}$

Különleges esetekben d. azaz a kapcsolatok kategóriája. ${\ displaystyle (H, +, \ cdot) = (\ {0,1 \}, \ lor, \ land)}$${\ displaystyle {\ mathcal {C}} = \ mathbf {Rel}}$${\ displaystyle {\ mathcal {C}}}$

használat

Az egész relációkra vonatkozó műveleteket relációs algebrában vizsgáljuk. Az informatikában a kapcsolatok fontosak a relációs adatbázisokkal való munka során .

Lásd még

• Kongruencia reláció
• Predikátum (logika)

irodalom

• Garrett Birkhoff : Rácselmélet . 3. Kiadás. AMS, Providence, RI 1973, ISBN 0-8218-1025-1 . 
• Stefan Brass: Matematikai logika adatbázis -alkalmazásokkal . Martin Luther Egyetem Halle-Wittenberg, Számítástechnikai Intézet, Halle 2005, p. 176 ( informatik.uni-halle.de [PDF]). 
• Erné Marcel: Bevezetés a rendelméletbe . Bibliographisches Institut, Mannheim 1982, ISBN 3-411-01638-8 . 
• Helmuth Gericke: Egyesületek elmélete . Bibliográfiai Intézet, Mannheim 1963. 
• Dieter Klaua : halmazelmélet . De Gruyter, Berlin / New York 1979, ISBN 3-11-007726-4 (A szerző a megfelelés kifejezést halmazelméleti értelemben használja a reláció szinonimájaként , de a szimbólum helyett . A cikkben azonban ill. (grafikonja ) írva).${\ displaystyle F}$${\ displaystyle R}$${\ displaystyle R}$${\ displaystyle G_ {R}}$${\ displaystyle R}$ 
• H. König: A termelési létesítmények vezérlésének tervezése és szerkezeti elmélete (=  ISW Research and Practice . Volume 13 ). Springer, Berlin / Heidelberg 1976, ISBN 3-540-07669-7 , pp. 15-17 , doi : 10.1007 / 978-3-642-81027-5_1 . 
• Ingmar Lehmann , Wolfgang Schulz: Halmazok - kapcsolatok - függvények . Világos bevezető. 3., átdolgozott és bővített kiadás. Vieweg + Teubner, Wiesbaden 2007, ISBN 978-3-8351-0162-3 . 
• Heike Mildenberger: Axiomatikus halmazelmélet . Freiburgi Egyetem, 2015. november 9., p. 58 ( mathematik.uni-freiburg.de [PDF]). 
• Willard van Orman Quine : Halmazelmélet és logikája (=  a matematika logikája és alapjai . Kötet 10 ). Vieweg + Teubner, Wiesbaden 1973, ISBN 3-528-08294-1 , pp. 264 (Amerikai angol: Set Theory And Its Logic . Cambridge, MA 1963. Ullstein 1978 papírkötés). 
• Gerard O'Regan: Útmutató a diszkrét matematikához. Halmazok, kapcsolatok és függvények (=  szövegek a számítástechnikában (TCS) ). Springer, Svájc 2016, p. 25–51 , doi : 10.1007 / 978-3-319-44561-8_2 ( springer.com [PDF; 1000 kB ]). 
• Fritz Reinhardt, Heinrich Soeder: dtv atlasz matematika . 11. kiadás. szalag 1 : Alapok, algebra és geometria. Deutscher Taschenbuchverlag, München 1998, ISBN 3-423-03007-0 , p. 30-33, 42-45 . 
• Gunther Schmidt, Thomas Ströhlein: Kapcsolatok és grafikonok . Springer, Berlin és mtsai. 1989, ISBN 3-540-50304-8 . 
• Robert Wall: Bevezetés a logikába és a matematikába nyelvészek számára . szalag 1 : Logika és halmazelmélet . Könyvtáros, Kronberg / Ts. 1974, ISBN 3-589-00023-6 . 
• Siegfried Wendt: Az információs technológia nem fizikai alapjai - értelmezett formalizmusok . 2. kiadás. Springer, Berlin / Heidelberg 2013, ISBN 978-3-540-54452-4 , doi : 10.1007 / 978-3-642-87627-1 ( books.google.de ). 

web Linkek

• Relációs irodalom a Német Nemzeti Könyvtár katalógusában
• Videó: A két számjegyű kapcsolatok ötlete . University of Education Heidelberg (PHHD) 2012, elérhetővé tette a Műszaki Információs Könyvtár (TIB), doi : 10.5446 / 19788 .

Egyedi hivatkozások és megjegyzések

1. ↑ ^{a b} G. Smolka: Programozás: 2. fejezet - Halmazelmélet , itt: Saarlandi Egyetem, 2003. május 20., 2.5. Bináris kapcsolatok, 15. o.
2. ^ Walter Gellert, Herbert Kästner , Siegfried Neuber (szerk.): Lexicon of Mathematics. Bibliographisches Institut Leipzig, 1979, 484. o.
3. ↑ ^{a b} Albert Monjallon: bevezetés a modern matematikába. 2. kiadás. Springer-Verlag, 2013, ISBN 978-3-663-16043-4 , 74. o. Doi: 10.1007 / 978-3-663-16043-4 , (books.google.de)
4. ↑ ^{a b} Wilhelm Dangelmaier: Gyártáselmélet 1: Módszertani alapismeretek. Springer-Verlag, 2017, ISBN 978-3-662-54922-3 , 478. o. Doi: 10.1007 / 978-3-662-54923-0 (books.google.de)
5. ↑ ^{a b} Cobocards: előterület és utóterület .
6. ↑ ^{a b} Matheboard: Kapcsolatok: Mit jelent pontosan a reláció előtti / utáni tartománya?
7. ↑ Dieter Klaua: Halmazelmélet . 62. oldal, 5. definíció (1. rész).
8. ↑ ^{a b c} H. König: A termelési létesítmények vezérlésének tervezése és szerkezetelmélete. 19. oldal.
9. ↑ További jelölések:, az angol nyelvű szakirodalomban :, lásd: Gerard O'Regan: Sets, Relations and Functions. 36. o.${\ displaystyle V_ {R}, V (R)}$${\ displaystyle \ operatornév {dom} R}$
   
10. ↑ Dieter Klaua: Halmazelmélet . 62. oldal, 5. definíció, (2. rész).
11. ↑ További jelölések:, az angol nyelvű szakirodalomban :, lásd: Gerard O'Regan: Sets, Relations and Functions. 36. o.${\ displaystyle N_ {R}, N (R)}$${\ displaystyle \ operatornév {rng} R}$
    
12. ↑ Dieter Klaua: Halmazelmélet . 62. oldal, 5. definíció, (3. rész).
13. ↑ Az algebrai struktúrák elméletében - különös tekintettel a kategóriaelméletre, a domain és a codomain kifejezéseket többnyire a forrás- és célhalmazok értelmében használják, míg a halmazelmélet bevezető írásaiban ezeket általában archetípusokként és képekként határozzák meg,
14. ↑ is jelentené hasonló , mennyiségi módon , hogy ger.: Bal keskeny vagy set-szerű nevű lásd Wikikönyvek: Matematika Szójegyzék: Matematikai tulajdonságok: kis elődje
15. ↑ Heike Mildenberger 2015, 59f.
16. ↑ Martin Ziegler: Előadás a halmazelméletről , Freiburgi Egyetem, 1992–2014, 12. o.
17. ↑ Azriel Levy: Basic Set Theory (= Dover Books on Mathematics . 13. kötet). Courier Corporation, Newburyport 2012, ISBN 978-0-486-15073-4 , 22. o., (Online)
18. ↑ Ha a primitív elemek megengedettek: a primitív elemekhez is van halmaz.${\ displaystyle b}$${\ displaystyle \ {a \ in A \ mid a \ in b \} = \ emptyyset}$
19. ↑ Lásd még: Axiomatic Set Theory, Getting a model of (ZF - Fnd) ∪ {¬Fnd} from the model of ZF , Ben Gurion University (BGU) of the Negev, The Department of Mathematics, 2003.
20. ↑ Az általános esetben a támogatási összeg szekvenciát a Allrelation , a homogén esetben, az n -szer a támogatási összeg van  .${\ displaystyle A = (A_ {i}) _ {i \ in \ {1, \ dot n \}}}$${\ displaystyle \ mathrm {U} _ {A} = \ texttyle \ prod A}$${\ displaystyle A}$${\ displaystyle U_ {A} = A ^ {n}}$
21. ↑ Stefan Brass (2005), 19. o.
22. ↑ A jellemző függvény, mint igazságfüggvény tehát egy logikai predikátumnak felel meg , és a modellelméletben a relációs szimbólumokat ezért predikátum szimbólumoknak is nevezik, lásd Stefan Brass (2005) 16. o.
23. ↑ Angol: előre relációs összetétel
24. ↑ Matematikai veremcsere: Előre és hátra összetétel a relációs algebrában . A Maplet jelölést néha rendelt pároknál használják :${\ displaystyle x \ mapsto y \ equiv (x, y)}$
25. ↑ ^{a b c} A Z jelölés szószedete §Kapcsolatok , Washingtoni Egyetem
26. ↑ Időnként a pontosvessző is megjelenik a vázlatos ábrázolásban. A hardvertől és a beállításoktól függően azonban nem mindig jelenik meg helyesen a Wikipédiában.
    ${\ displaystyle R {\ mbox {⨟}} S}$
27. ↑ Angol: visszafelé relációs összetétel
28. ↑ ^{a b} H. König: A termelési létesítmények vezérlésének tervezése és szerkezetelmélete. 21. oldal.
29. ↑ ^{a b c} W. v. O. Quine: Halmazelmélet és logikája. 47. oldal.
30. ^ Relációs algebra. In: Mathepedia.de.
31. ↑ Szintén bijection .${\ displaystyle \ pi \ kettőspont \ {1,2, \ dotsc, n \} \ operatornév {\ twoheadrightarrow \! \! \! \! \! \! \! \! \! \! \! \; \; \ rightarrowtailtail} \ {1,2, \ dotsc, n \}}$
32. ↑ A jelöléseket lásd Gary Hardegree: Halmazelmélet, 2. fejezet: Kapcsolatok , Massachusettsi Egyetem, Amherst, Filozófia Tanszék, 2015. ősz, 11. o .: D16 és D17. A többi jelöléssel ellentétben ezek a szimbólumok a tápegységek közötti képekre (funkciókra) hivatkoznak .${\ displaystyle R ^ {\ to}, R ^ {\ leftarrow}}$${\ displaystyle {\ mathcal {P}} (A), {\ mathcal {P}} (B)}$
33. ↑ Analóg: D. Klaua: Halmazelmélet . 63. o., 6. definíció (a).
34. ↑ A rendi viszonyok és hasonlók esetében egyes szerzők elődhalmazról vagy osztályról is beszélnek, lásd Heike Mildenberger 2015, 6. o., 1.12. Definíció.
35. ↑ W. v. O. Quine: Halmazelmélet és logikája. 17. oldal Figyelem: A nyomat címmel a kép , de egyértelműen meghatározza a eredeti kép (egy a bal oldali koordináta = érveket ). Meg kell jegyezni, hogy ezt a jelölést itt a funkciókkal ellentétben használják, a függvényekkel a funkció alatti halmaz képét (jobb oldali koordináták halmaza = funkcióértékek ) jelenti . A függvények különleges kapcsolatok. Lásd a képet (matematika) §Alternatív jelölések .${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle f}$
36. ↑ Johannes Köbler: Bevezetés a számítógépes elméletekbe: kapcsolatok. Humboldt Egyetem Berlin, Számítástechnikai Intézet WS2013 / 14, 68. o.
37. ↑ W. v. O. Quine: Halmazelmélet és logikája. 17. oldal.
38. ↑ A fenti részletes kapcsolati definíciót követve az átló az identitás gráfja: (Kapcsolat) és (Graph).${\ displaystyle \ mathrm {I} _ {A} = (\ Delta _ {A}, A, A)}$${\ displaystyle \ Delta _ {A} = \ {(a, a) \ mid a \ in A \}}$
39. ↑ Követve a fenti részletes kapcsolatban definíció, amely analóg a diagonális, a Nabla fogják érteni, mint a grafikonon az összes kapcsolatban: (kapcsolat) a (grafikon)${\ displaystyle \ mathrm {U} _ {A} = (\ nabla _ {A}, A, A)}$${\ displaystyle \ nabla _ {A} = A \ alkalommal A}$
40. ↑ Ez ahhoz vezethet, hogy zavart a Descartes-szorzat a vezetést. A jelentés minden esetben a szövegkörnyezetből adódik.${\ displaystyle R ^ {n} = R_ {1} \ times \ dotb \ times R_ {n}}$${\ displaystyle R = R_ {1} = \ dotb = R_ {n}}$
41. ^ ^{A b} Gerard O'Regan: Halmazok, kapcsolatok és függvények. 39. o.
42. ↑ Lásd még: Kleenesche boríték .
43. ↑ Ezeknek az asszociációknak a tranzitivitási tulajdonságait lásd : A tranzitív reláció bizonyítása az A${\ displaystyle \ bigcup _ {n = 1} ^ {\ infty} R ^ {n}}$ -n, on: StackExchange: Mathematics 2018.
44. ↑ Robin Hirsch, Ian Hodkinson: Kapcsolati algebrák. P. 7, on: Harmadik indiai konferencia a logikáról és alkalmazásairól (ICLA). 7-11 2009. január, Chennai, India.
45. ↑ A linkek közül (egyjegyű) és (kétjegyű) - szigorúan véve - a korlátozásokra vagy azokra gondolunk.${\ displaystyle {} ^ {-}, {} ^ {\ smallsmile}}$${\ displaystyle \ cap, \ cup, \ circ}$${\ displaystyle A}$${\ displaystyle A ^ {2}}$
46. ^ C. Brink, K. Britz, RA Schmidt: Peirce Algebras. (1994), 163f. In: M. Nivat, C. Rattray, T. Rus, G. Scollo (szerk.): Algebrai módszertan és szoftver technológia (AMAST'93). Műhelyek a számítástechnikában. Springer, London.
47. ↑ A gráfelméleti értelemben vett gráf kifejezést meg kell különböztetni a reláció gráf terminusától az elején említett relációk részletes definíciója (valamint a képek) szerint, amelyet a gráfelmélet nem használ.
48. ↑ A szín kifejezés abból fakad, hogy a multimetriai elmélet szerint sokszorosságként értelmezett szám a grafikus ábrázolásban az él számkódolt színeként jelenik meg , hasonlóan a színes csomópontokkal . Példa a színszámokra a RAL színek .${\ displaystyle f (v)}$${\ displaystyle v}$${\ displaystyle e}$
    
49. ↑ WD Blizard: Valódi értékű multiset és fuzzy set. In: Fuzzy Sets and Systems. 33. kötet, 1989, 77-97. doi: 10.1016 / 0165-0114 (89) 90218-2 .
50. ↑ „Két mennyiség, amelyek egyenlők egy és ugyanaz a harmadik, egyenlők egymással.” Vö.
    Henri Poincaré: Wissenschaft und Hypothese. Szerző. Német kiadás ext. Jegyzet ettől F. és L. Lindemann. Teubner, Lipcse 1904, 36. o.
51. ↑ Wolfgang Rautenberg: Bevezetés a matematikai logikába. Tankönyv. Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8348-0578-2 , 42. o.
52. ↑ Az 1. axióma az Eukleidész Elemek lehet, másrészt, is tekinthető egyenértékűnek harmadik egyenlők .
53. ↑ Ez nem ritka, hogy a KNX kell meghatározni , mint a teljes .
54. ↑ Ez könnyen látható a fenti táblázatokból (1. és 2. oszlop), figyelembe véve , pl. H. és a predikátum logikai szabályai. Az inverziók az involutivitás miatt érvényesek .${\ displaystyle \ neg (aRb) \ iff a {\ overline {R}} b}$${\ displaystyle \ neg (a, b) \ in R \ iff (a, b) \ not \ in R \ iff (a, b) \ in {\ overline {R}}}$${\ displaystyle {\ overline {\ overline {R}}} = R}$
55. ↑ Wendt 2013, 31. oldal