Transzitív viszony

Két transzitív és egy nem transzitív reláció (jobb alsó sarokban) az irányított grafikonok szerint

A tranzitív reláció van matematika kétszámjegyű kapcsolatban a mennyiség , amely a három elem, hogy az a tulajdonsága , , mennyisége és mindig következik. Transzitív kapcsolatok például az egyenlő és a kisebb kapcsolatok a valós számokon , mert három valós szám esetén , és a és mindig vonatkozik rá , és onnan és következik . ${\ displaystyle R}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle z}$${\ displaystyle xRy}$${\ displaystyle yRz}$${\ displaystyle xRz}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle z}$${\ displaystyle x = y}$${\ displaystyle y = z}$${\ displaystyle x = z}$${\ displaystyle x <y}$${\ displaystyle y <z}$${\ displaystyle x <z}$

A nem tranzitív relációt intranzitívnek nevezzük (nem tévesztendő össze a negatív transzitivitással ). A tranzitivitás az egyik előfeltétele az ekvivalencia relációnak vagy a rend relációnak .

Formális meghatározás

Ha van egy halmaz és egy kétjegyű reláció , akkor tranzitívnak mondjuk, ha (az infix jelöléssel ): ${\ displaystyle M}$${\ displaystyle R \ subseteq M \ szor M}$${\ displaystyle M}$${\ displaystyle R}$

${\ displaystyle \ forall x, y, z \ M-ben: xRy \ land yRz \ Rightarrow xRz.}$

Ábrázolás irányított gráfként

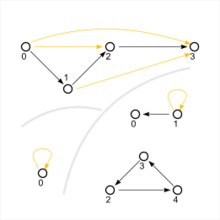
Bármilyen kapcsolatban egy sor lehet tekinteni, mint egy irányított gráf (lásd a fenti példát). A grafikon csomópontjai a elemei . Az irányított él (nyíl ) csomópontról csomópontra akkor és csak akkor húzódik meg, ha érvényes. ${\ displaystyle R}$${\ displaystyle M}$${\ displaystyle M}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle a \ longrightarrow b}$${\ displaystyle aRb}$

A transzitivitása a grafikonon a következőképpen jellemezhető: Amikor két nyíl követi egymást ( ), van egy nyíl is, amely közvetlenül összeköti a kezdő és a vég csomópontot ( ) (ez a helyzet a Hasse-diagramon is ). ${\ displaystyle R}$${\ displaystyle a \ longrightarrow b \ longrightarrow c}$${\ displaystyle a \ longrightarrow c}$

tulajdonságait

• A reláció transzitivitása lehetővé teszi a következtetések levonását is több lépésben (amit a teljes indukció is könnyen megmutat ): ${\ displaystyle R}$

  ${\ displaystyle a \, R \, b_ {1} \, R \, b_ {2} \, R \, \ pöttyök \, R \, b_ {n} \, R \, c \ jelentése \, R \, c}$

• A kapcsolatok láncolásának segítségével a tranzitivitást a következő feltétel is jellemezheti: ${\ displaystyle \ circ}$

  ${\ displaystyle R \ circ R \ subseteq R}$

• Ha a reláció tranzitív, akkor ez a fordított relációra is érvényes . Példák: a kapcsolat túl ellentétes, a kapcsolat túl ellentétes .${\ displaystyle R}$ ${\ displaystyle R ^ {- 1}}$${\ displaystyle \ leq}$${\ displaystyle \ geq}$${\ displaystyle <\}$${\ displaystyle> \}$
• Ha a kapcsolatok és tranzitívak, akkor ez vonatkozik a kereszteződésükre is . Ez az állítás két viszonytól a transzitív kapcsolatok bármely családjának metszéspontjáig általánosítható.${\ displaystyle R}$${\ displaystyle S}$ ${\ displaystyle R \ cap S}$${\ displaystyle \ cap _ {i \ I} R_ {i}} -ban$
• Minden önkényes kapcsolatban van egy legkisebb tranzitív reláció , hogy tartalmazza az úgynevezett tranzitív borítékot az . Példa: az előd reláció legyen a természetes számok halmazán, így érvényes . Maga a kapcsolat nem transzitív. A kisebb összefüggés a .${\ displaystyle R}$${\ displaystyle S}$${\ displaystyle R}$${\ displaystyle R}$
  ${\ displaystyle R}$${\ displaystyle a \, R \, b: \ Longleftrightarrow a = b-1}$${\ displaystyle R}$${\ displaystyle R}$${\ displaystyle <\}$

Példák

A valós számok sorrendje

Az a> b és a b> c pontból következik az a> c

A kisebb képest a valós számok tranzitív, mert következik re és . Ez is szigorú totális rend . ${\ displaystyle <\}$${\ displaystyle x <y}$${\ displaystyle y <z}$${\ displaystyle x <z}$

Hasonlóképpen, a kapcsolatok , és tranzitív. ${\ displaystyle> \}$${\ displaystyle \ leq \}$${\ displaystyle \ geq \}$

A valós számok egyenlősége

Rendes egyenlőség valós számokon tranzitív, mert következik re és . Ez egy ekvivalencia reláció is . ${\ displaystyle = \}$${\ displaystyle x = y}$${\ displaystyle y = z}$${\ displaystyle x = z}$

Az egyenlőtlenség vonatkozásában a valós számok azonban nem tranzitív: és , de természetesen nem érvényes. ${\ displaystyle \ neq}$${\ displaystyle 3 \ neq 5}$${\ displaystyle 5 \ neq 3}$${\ displaystyle 3 \ neq 3}$

Az egész számok oszthatósága

Az oszthatóság kapcsolatban az egész tranzitív, mert következik re és . Ez egy kvázi megrendelés is . Ha a természetes számok halmazára korlátozódik, részleges sorrendet kap . ${\ displaystyle |}$${\ displaystyle a | b}$${\ displaystyle b | c}$${\ displaystyle a | c}$

Például nem transzitív a kopimum . Tehát és társprimák, ugyanúgy, és mégis, és megvan a közös tényezőjük . ${\ displaystyle 12}$${\ displaystyle 5}$${\ displaystyle 5}$${\ displaystyle 9}$${\ displaystyle 12}$${\ displaystyle 9}$ ${\ displaystyle 3}$

Részhalmaz

A halmazok közötti részhalmaz viszonya tranzitív, mert a és alapján következik . Ezenkívül részleges megrendelés. ${\ displaystyle \ subseteq}$${\ displaystyle A \ subseteq B}$${\ displaystyle B \ subseteq C}$${\ displaystyle A \ subseteq C}$${\ displaystyle \ subseteq}$

Például a halmazok szétválasztása nem tranzitív . Tehát a halmazok és diszjunkt, csakúgy, mint a és , de nem és (mivel az 1 elem közös bennük). ${\ displaystyle \ lbrace 1,2 \ rbrace}$${\ displaystyle \ lbrace 3 \ rbrace}$${\ displaystyle \ lbrace 3 \ rbrace}$${\ displaystyle \ lbrace 1,4 \ rbrace}$${\ displaystyle \ lbrace 1,2 \ rbrace}$${\ displaystyle \ lbrace 1,4 \ rbrace}$

Párhuzamos egyenesek

A geometria , amely párhuzamossága egyenes tranzitív: Ha mindkét az egyenes és párhuzamos és az egyenes vonalak , és ezután is , és párhuzamosan. Ezenkívül a párhuzamosság ekvivalencia reláció. ${\ displaystyle g_ {1}}$${\ displaystyle g_ {2}}$${\ displaystyle g_ {2}}$${\ displaystyle g_ {3}}$${\ displaystyle g_ {1}}$${\ displaystyle g_ {3}}$

Implikáció a logikában

A logikában a transzitivitás vonatkozik az implikációra , ahol ezt a predikátum logikában modus barbarának is nevezik :

Innen és következik (hasonlítsa össze még: metszésszabály ). ${\ displaystyle A \ Rightarrow B}$${\ displaystyle B \ Rightarrow C}$${\ displaystyle A \ Rightarrow C}$

Az implikáció kvázi sorrendet határoz meg a vizsgált logika képletein.

Lásd még

• Transzitív boríték
• Negatív transzitivitás

web Linkek

• Transzitivitás . In: Michiel Hazewinkel (Szerk.): Encyclopedia of Mathematics . Springer-Verlag és EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (angol, online ).