Diszkrét Fourier -transzformáció

A diszkrét Fourier -transzformáció (DFT) a Fourier -elemzés területéről származó transzformáció . Ez térképek egy időben diszkrét véges jelet , amely tovább periodikusan , rá egy diszkrét, periodikus frekvencia spektrum , amely szintén nevezik képterület . A DFT nagy jelentőséggel bír a digitális jelfeldolgozásban a jelfeldolgozás szempontjából. Itt az űrlapon optimalizált változatok a használt gyors Fourier -transzformáció ( angolul gyors Fourier -transzformáció , FFT ) és inverzeik.

A DFT -t számos feladatra használják a jelfeldolgozásban, például: B.

• a mintavételezett jelben előforduló frekvenciák meghatározása ,
• az amplitúdók és a hozzájuk tartozó fázisviszonyok meghatározása ezekhez a frekvenciákhoz,
• nagy szűrőhosszúságú digitális szűrők megvalósításához .

Az inverz DFT -vel, röviden iDFT -vel az időtartományban lévő jel rekonstruálható a frekvenciakomponensekből. A DFT és az iDFT összekapcsolásával egy jel manipulálható a frekvenciatartományban, ahogy az ekvalizerben is használatos . A diszkrét Fourier-transzformációt meg kell különböztetni a rokon Fourier-transzformációtól az idő-diszkrét jelek esetében (angol discrete-time Fourier-transzformáció, DTFT ), amely folyamatos frekvenciaspektrumot képez az idődiszkrét jelekből.

meghatározás

Diszkrét Fourier -transzformáció (DFT)

A diszkrét Fourier-transzformáció feldolgozza a számsorozatot , amely például időbeli diszkrét mért értékként keletkezett . Feltételezzük, hogy ezek a mért értékek egy periodikus jel időszakának felelnek meg. A DFT abban az esetben is alkalmazható, ha komplex számok vannak, azaz:${\ displaystyle a = (a_ {0}, \ dotsc, a_ {N-1})}$${\ displaystyle a}$${\ displaystyle a = (a_ {0}, \ dotsc, a_ {N-1}) \ in \ mathbb {C} ^ {N}}$

Az átalakítás eredménye a szekvencia felbontása harmonikus (szinuszos) komponensekre és egy "állandó komponensre", amely megfelel a bemeneti sorozat átlagos értékének. Az eredmény az úgynevezett „diszkrét Fourier-transzformáció” a . Az együtthatók a bomlási komponensek amplitúdói. Az egyik Fourier -együtthatókat vagy Fourier -komponenseket is hív . ${\ displaystyle {\ hat {a}} _ {0}}$${\ displaystyle {\ hat {a}} = ({\ hat {a}} _ {0}, \ dotsc, {\ hat {a}} _ {N-1}) \ in \ mathbb {C} ^ { N}}$${\ displaystyle a}$${\ displaystyle {\ hat {a}}}$${\ displaystyle {\ hat {a}} _ {k}}$

A frekvenciakomponensek / fázishelyzet meghatározásakor általában a poláris forma kompakt matematikai jelölését használják ( Euler -képlet ):

${\ displaystyle \ mathrm {e} ^ {\ mathrm {i} \, \ phi} = \ cos \ left (\ phi \ right) + \ mathrm {i} \, \ sin \ left (\ phi \ right)}$

A Fourier -együtthatókat a bemeneti sorrendből számítják ki: ${\ displaystyle {\ hat {a}} _ {k}}$

${\ displaystyle {\ hat {a}} _ {k} = \ sum _ {j = 0} ^ {N-1} \ mathrm {e} ^ {- 2 \ pi \ mathrm {i} \ cdot {\ frac {jk} {N}}} \ cdot a_ {j}}$   számára   ${\ displaystyle k = 0, \ dotsc, N-1}$

Az egyenlet mátrix-vektor szorzatként is felírható :

${\ displaystyle {\ hat {a}} = W \ cdot a}$   val vel   ${\ displaystyle W [k, j] = \ mathrm {e} ^ {- 2 \ pi \ mathrm {i} \ cdot {\ frac {jk} {N}}}}$

A szimmetrikus transzformációs mátrixot a dimenzióval "Fourier mátrixnak" nevezik. ${\ displaystyle W}$${\ displaystyle N \ x N}$

Inverz diszkrét Fourier -transzformáció (iDFT)

A szinuszos bomlási komponensek összege adja meg az eredeti bemeneti sorrendet . ${\ displaystyle a}$

Ebből a célból, az átalakulás eredménye használatos , mint egy együtthatót egy polinomiális , azzal a amplitúdók képviselő kapcsolódó harmonikus rezgéseket . ${\ displaystyle {\ hat {a}}}$${\ displaystyle {\ hat {a}} _ {k}}$${\ displaystyle z_ {k}}$

${\ displaystyle A (z_ {k}) = {\ tfrac {1} {N}} \ left ({\ hat {a}} _ {0} z_ {k} ^ {0} + {\ hat {a} } _ {1} z_ {k} ^ {1} + \ pontok + {\ kalap {a}} _ {N-1} z_ {k} ^ {N-1} \ jobb) \;.}$

Az érvek vannak egyenletesen elosztva pontot a készüléken kör a komplex szám sík , i. H. az egység gyökerei${\ displaystyle z_ {0}, z_ {1}, \ dotsc, z_ {N-1}}$${\ displaystyle N}$${\ displaystyle N}$

${\ displaystyle z_ {k} = \ mathrm {e} ^ {{\ frac {2 \ pi \ mathrm {i}} {N}} k} = \ cos \ left ({\ tfrac {2 \ pi} {N }} k \ jobb) + \ mathrm {i} \, \ sin \ bal ({\ tfrac {2 \ pi} {N}} k \ jobb) \;.}$

Ez a magyarázat a diszkrét Fourier -transzformáció és a z -transzformáció közötti kapcsolatot is mutatja . A fő különbség az, hogy a z-transzformáció nem korlátozódik az egységkörre, ezért időbeli dinamikus folyamatokat is leképezhet.

Az eredeti sorozat együtthatói meghatározhatók a Fourier -együtthatókból az iDFT segítségével : ${\ displaystyle a}$${\ displaystyle {\ hat {a}} _ {j}}$

${\ displaystyle a_ {k} = {\ frac {1} {N}} \ sum _ {j = 0} ^ {N-1} \ mathrm {e} ^ {2 \ pi \ mathrm {i} \ cdot { \ frac {jk} {N}}} \ cdot {\ hat {a}} _ {j}}$   számára   ${\ displaystyle k = 0, \ dotsc, N-1}$

A jelölésben mint mátrix-vektor termék :

${\ displaystyle a = W ^ {- 1} \ cdot {\ hat {a}}}$   val vel   ${\ displaystyle W ^ {- 1} [k, j] = {\ frac {1} {N}} \ mathrm {e} ^ {2 \ pi \ mathrm {i} \ cdot {\ frac {jk} {N }}}}$

ahol itt azt megszorozzuk az inverz mátrixot a . ${\ displaystyle {\ hat {a}}}$${\ displaystyle W}$

Időszakos periodikus függvény meghatározása a bemeneti sorrend alapján

Az időfüggő függvény meghatározható az inverz diszkrét Fourier-transzformációból is, amely az idődiszkrét mért értékeken (a bemeneti sorrenden) keresztül vezet:

Ebből a célból a polinom egy függvényhez kapcsolódik, amely egyenletesen forog az egységkör körül . Ennek eredményeképpen egy időben folyamatos periodikus függvény jön létre${\ displaystyle A (z)}$${\ displaystyle z (t) = \ mathrm {e} ^ {\ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}}}$

${\ displaystyle f (t) = A (z (t)) = {\ tfrac {1} {N}} \ left ({\ hat {a}} _ {0} + {\ hat {a}} _ { 1} \ mathrm {e} ^ {\ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}} + {\ kalap {a}} _ {2} \ mathrm {e} ^ {2 \ cdot \ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}} + \ dotsb + {\ hat {a}} _ {N-1} \ mathrm {e } ^ {(N-1) \ cdot \ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}} \ jobb),}$

amely időnként csak feltételezi a függvény értékeit. ${\ displaystyle t_ {k} = t_ {0} + {\ tfrac {k} {N}} T}$${\ displaystyle a_ {k} = A (z_ {k})}$

A hatalomnak van formája ${\ displaystyle z (t)}$

${\ displaystyle z (t) ^ {k} = \ mathrm {e} ^ {k \ cdot \ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}} = \ cos ( 2k \ pi {\ tfrac {t-t_ {0}} {T}}) + \ mathrm {i} \, \ sin (2k \ pi {\ tfrac {t-t_ {0}} {T}})}$

és ezért az időszak és a frekvencia vagy a szögfrekvencia . Így a mért értékek sorrendjét ábrázolja és interpolálja egy állandó szint szuperpozíciója , egy alapvető oszcilláció a és harmonikusok között . ${\ displaystyle T / k}$${\ displaystyle k / T}$${\ displaystyle 2k \ pi / T}$${\ displaystyle k = 0}$${\ displaystyle k = 1}$${\ displaystyle k> 1}$

A fent megadott interpolációs függvény nem az egyetlen, amely ily módon felépíthető. Bármelyik funkció

${\ displaystyle {\ begin {mátrix} f (t) = {\ frac {1} {N}} & \ left ({\ hat {a}} _ {0} + {\ hat {a}} _ {1 } \ mathrm {e} ^ {\ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}} + {\ hat {a}} _ {2} \ mathrm {e} ^ {2 \ cdot \ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}} + \ pöttyök + {\ kalap {a}} _ {M-1} \ mathrm {e} ^ {(M-1) \ cdot \ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}} \ jobb. \\ & \ bal. + {\ Hat {a}} _ {M} \ mathrm {e} ^ {(MN) \ cdot \ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}} + \ pontok + {\ kalap {a} } _ {N-1} \ mathrm {e} ^ {(N-1-N) \ cdot \ mathrm {i} 2 \ pi {\ frac {t-t_ {0}} {T}}} \ jobb) \ end {mátrix}}}$

rendelkezik ezzel az interpolációs tulajdonsággal.

Különleges eset: DFT valódi vektor esetén

A Fourier -transzformációhoz hasonlóan a szimmetria bizonyos törvényei is érvényesek a DFT -re. Így válik a periódusból származó valódi jel Hermit -jelvé ( ) a frekvenciatartományban: ${\ displaystyle g (- {\ vec {x}}) = {\ overline {g ({\ vec {x}})}}}$

${\ displaystyle {\ hat {a}} _ {Nk} = {\ overline {{\ hat {a}} _ {k}}}}$

Ez azt jelenti, hogy a frekvenciatartományban csak független komplex együtthatók vannak . Ez a tény felhasználható a DFT megvalósításakor, ha ismert, hogy a bemeneti jel tisztán valós. Az eredmény ábrázolásához nem (mint a teljes DFT esetében), de csak komplex számok szükségesek. A többi komplex szám elemi számításokkal rekonstruálható (lásd a fenti képletet). A hermitikus szimmetria a jel középső elemére utal . ${\ displaystyle N / 2}$${\ displaystyle {\ hat {a}} _ {k}}$${\ displaystyle N}$${\ displaystyle N / 2}$${\ displaystyle N / 2}$${\ displaystyle k = N / 2}$${\ displaystyle {\ hat {a}} _ {k}}$

Bizonyítás: Mivel Euler személyazonosságát , és mert a valós helyzet : ${\ displaystyle \ mathrm {e} ^ {2 \ pi \ mathrm {i}} = 1}$${\ displaystyle {\ overline {\ mathrm {e} ^ {\ mathrm {i} \ phi}}} = \ mathrm {e} ^ {- \ mathrm {i} \ phi}}$${\ displaystyle a \ in \ mathbb {R} ^ {N}}$

${\ displaystyle {\ hat {a}} _ {Nk} = \ sum _ {j = 0} ^ {N-1} \ mathrm {e} ^ {- 2 \ pi \ mathrm {i} \ cdot {\ frac {Nj} {N}}} \ mathrm {e} ^ {2 \ pi \ mathrm {i} \ cdot {\ frac {jk} {N}}} \ cdot a_ {j} = \ összeg _ {j = 0 } ^ {N-1} {\ overline {\ mathrm {e} ^ {- 2 \ pi \ mathrm {i} \ cdot {\ frac {jk} {N}}} \ cdot a_ {j}}} = { \ overline {{\ hat {a}} _ {k}}}}$

Ezzel szemben, a következő érvényes megfelelően: Ha a feltétel minden is teljesül, az inverz DFT egy igazi vektor . ${\ displaystyle {\ hat {a}} \ in \ mathbb {C} ^ {N}}$${\ displaystyle {\ hat {a}} _ {Nk} = {\ overline {{\ hat {a}} _ {k}}}}$${\ displaystyle k = 1, \ dotsc, N-1}$${\ displaystyle {\ hat {a}} _ {0} \ in \ mathbb {R}}$${\ displaystyle a \ in \ mathbb {R} ^ {N}}$

Általánosítás: A DFT matematikai meghatározása

A matematikában a diszkrét Fourier -transzformációt nagyon általános kontextusban tekintik. Többek között a számítógépes algebrában használják nagyszámú hatékony algoritmus számára a pontos aritmetika számára , például egész számok gyors szorzására a Schönhage-Strassen algoritmussal .

Legyen egy kommutatív egységes gyűrű , amelyben a szám (vagyis az szeres összege ) egy egységet . Továbbá van egy primitív -edik egységgyök . A diszkrét Fourier-transzformáltja tuple ezután által ${\ displaystyle R}$ ${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle 1}$${\ displaystyle R}$${\ displaystyle N}$ ${\ displaystyle w}$${\ displaystyle a = (a_ {0}, \ dotsc, a_ {N-1}) \ in R ^ {N}}$ ${\ displaystyle {\ hat {a}}}$

${\ displaystyle {\ hat {a}} _ {k} = \ sum _ {j = 0} ^ {N-1} w ^ {- \, j \ cdot k} \ cdot a_ {j}}$ számára ${\ displaystyle k = 0, \ dotsc, N-1}$

magyarázta. A feltételezések szerint létezik az együtthatókkal rendelkező diszkrét inverz Fourier -transzformáció is${\ displaystyle {\ hat {a}} \ in R ^ {N}}$ ${\ displaystyle a}$

${\ displaystyle a_ {k} = {1 \ over N} \ sum _ {j = 0} ^ {N-1} w ^ {j \ cdot k} \ cdot {\ hat {a}} _ {j}}$számára .${\ displaystyle k = 0, \ dotsc, N-1}$

A rendkívül fontos speciális esetben az egység -gyökét szokták használni a DFT -hez . Ez adja az első szakasz képletét. ${\ displaystyle R = \ mathbb {C}}$${\ displaystyle N}$${\ displaystyle w = \ exp \ left (2 \ pi \, \ mathrm {i} / N \ right)}$

Többdimenziós DFT

A DFT könnyen kiterjeszthető többdimenziós jelekre. Ezután egyszer alkalmazzák az összes koordináta -irányra. A két dimenzió fontos speciális esetére ( képfeldolgozás ) például a következők vonatkoznak:

${\ displaystyle {\ hat {a}} _ {k, l} = \ sum _ {m = 0} ^ {M-1} \ sum _ {n = 0} ^ {N-1} a_ {m, n } \ cdot \ mathrm {e} ^ {- 2 \ pi \ mathrm {i} \ cdot {\ frac {mk} {M}}} \ mathrm {e} ^ {- 2 \ pi \ mathrm {i} \ cdot {\ frac {nl} {N}}}}$a és${\ displaystyle k = 0, \ dotsc, M-1}$${\ displaystyle l = 0, \ dotsc, N-1}$

Ennek megfelelően a fordított transzformáció:

${\ displaystyle a_ {m, n} = {\ frac {1} {MN}} \ sum _ {k = 0} ^ {M-1} \ sum _ {l = 0} ^ {N-1} {\ kalap {a}} _ {k, l} \ cdot \ mathrm {e} ^ {2 \ pi \ mathrm {i} \ cdot {\ frac {mk} {M}}} \ mathrm {e} ^ {2 \ pi \ mathrm {i} \ cdot {\ frac {nl} {N}}}}$a és${\ displaystyle m = 0, \ dotsc, M-1}$${\ displaystyle n = 0, \ dotsc, N-1}$

Váltás és skálázás időben és gyakoriságban

A DFT és az iDFT számítási képleteiben az összegzés ( fenti indexváltozó ) egy eltolt tartományon is átfuthat, nem pedig túl , ha a vektort periodikusan folytatjuk az összes egész indexre, mert ez érvényes . Tehát tetszőlegesen mozgathatjuk az összegzési határokat, amíg a teljes számok hosszúságú szegmense le van fedve. ${\ displaystyle j}$${\ displaystyle 0, \ dotsc, N-1}$${\ displaystyle k, \ dotsc, N-1 + k}$${\ displaystyle \ texttyle a = (a_ {0}, \ dotsc, a_ {N-1})}$ ${\ displaystyle \ texttyle w ^ {N + k} = w ^ {k}}$${\ displaystyle N}$

Térjünk most vissza az összetett esethez. A gyakorlati alkalmazásokban az indexeket egyenlő távolságú időponttal kell összekapcsolni,

${\ displaystyle t_ {n}: = nT}$a ,${\ displaystyle n = 1-M, \ cdots, NM}$

amelynek hossza is van . Kívánatos továbbá frekvenciákat rendelni a számított együtthatókhoz, amelyek köré koncentrálódnak ${\ displaystyle N}$${\ displaystyle 0}$

${\ displaystyle \ omega _ {n}: = 2 \ pi {\ frac {n} {NT}}}$ számára ${\ displaystyle n = 1-K, \ dotsc, NK}$

és közel . ${\ displaystyle K}$${\ displaystyle N / 2}$

A kiválasztott időpontokban „mért” függvény eredményezi az együtthatókkal rendelkező megfigyelési vektort , amelynek DFT -jét figyelembe veszik a Fourier -elemzésben. Azután ${\ displaystyle f}$${\ displaystyle \ texttyle x \ in \ mathbb {C} ^ {N}}$${\ displaystyle \ texttyle x_ {n} = f (t_ {n})}$${\ displaystyle \ texttyle y_ {n} = {\ hat {f}} (\ omega _ {n}) = F (\ omega _ {n})}$

${\ displaystyle F (\ omega _ {n}) = \ sum _ {k = 1-M} ^ {NM} \ mathrm {e} ^ {- 2 \ pi \ mathrm {i} {\ frac {nkT} { NT}}} x_ {k} = \ sum _ {k = 1-M} ^ {NM} \ mathrm {e} ^ {- \ mathrm {i} \, \ omega _ {n} \ cdot t_ {k} } f (t_ {k})}$

és

${\ displaystyle f (t_ {n}) = x_ {n} = {\ frac {1} {N}} \ sum _ {k = 1-K} ^ {NK} \ mathrm {e} ^ {2 \ pi \ mathrm {i} {\ frac {nkT} {NT}}} y_ {k} = {\ frac {1} {N}} \ sum _ {k = 1-K} ^ {NK} \ mathrm {e} ^ {\ mathrm {i} \ omega _ {k} \ cdot t_ {n}} F (\ omega _ {k})}$.

Példák

A Fourier-transzformáció transzformáció függvényében , hogy egy ideig képviseletét a kölcsönös frekvencia térben . Ez vonatkozik az egy (1D), két (2D) vagy több térbeli irányban meghatározott pozíciófüggvényekre is. Ezeket térbeli frekvenciákká alakítják át a Fourier -transzformáció segítségével, minden irányban egymás után. A diffrakciós jelenségek az optikában vagy a röntgen-elemzésben közvetlenül értelmezhetők a Fourier-transzformáció intenzitáseloszlásaként. A fázisviszony általában elveszik a fotózásban. Csak a holográfia esetében rögzítik a fázisviszonyokat referencianyaláb egymásra helyezésével. ${\ displaystyle f (t)}$${\ displaystyle g (v) ^ {*}}$${\ displaystyle t}$ ${\ displaystyle v: = 1 / t}$

Egyszerű keret

2D Fourier transzformációk. Bal kimeneti kép, a Fourier -transzformáció jobb intenzitás eloszlása.

2D Fourier transzformációk. Bal kimeneti kép, a Fourier -transzformáció jobb intenzitás eloszlása.

A jobb oldali képek kétdimenziós Fourier-transzformációkat (2D FFT) ábrázolnak geometriai mintákon, négyzetekre számítva a diszkrét pixelméretet. A bal oldali képen képpont méretű rés látható , mellette a diffrakciós kép intenzitáseloszlása. A pozícióváltozót kölcsönös komplex értékekké alakítják át . A kiválasztott méreteknél egy képpont a kölcsönös képpontok kölcsönös értékévé alakul . A képpontok közötti rés szélessége a kölcsönös térben a méret , a magasság értékeként jelenik meg , magasabb rendű harmonikus frekvenciákkal. A számított diffrakciós képek a komplex változó intenzitáseloszlásait mutatják . Meg lehet állapítani, hogy csak a képinformációk felét hordozzák forgási szimmetriájuk alapján. ${\ displaystyle a \ alkalommal a}$${\ displaystyle e \ times f}$${\ displaystyle r}$${\ displaystyle r ^ {*}}$${\ displaystyle 1 / a}$${\ displaystyle e}$${\ displaystyle r ^ {*} = a / e}$${\ displaystyle r ^ {*} = a / f}$${\ displaystyle r ^ {*}}$

Az időszakos csúcsok egy négyzethullámú jel magasabb rendű térbeli frekvenciájának felelnek meg. Hasonló példák találhatók a Fourier -elemzés , a Fourier -transzformáció vagy a diffrakciós lemezek kulcsszavak alatt .

A második részben szabályos hatszög van hajlítva. Ismét az ábra mérete pontként jelenik meg a jobb oldali diffrakciós képen. A hatszoros szimmetria jól látható. A kezdeti kép eltolódása - szemben a forgatással - csak a fázisviszonyban lenne hatással, ami a kiválasztott ábrázoláson nem tekinthető intenzitáseloszlásnak.

Az alsó rész a jobb oldali háromszög kiszámított diffrakciós mintáját mutatja. A hatszoros szimmetriát csak szimulálják, ami látható a diffrakciós csillagok modulációjának hiányából.

A második képsorozat két kör alakú nyílás diffrakcióját hasonlítja össze. Egy nagy kör kis diffrakciós mintát hoz létre, és fordítva. Teleszkóp esetén a fény diffrakciója a lencse nyílásánál korlátozza a felbontást. Minél nagyobb az átmérő, annál kisebb a csillag diffrakciós mintázata, annál könnyebb megkülönböztetni a közel lévő csillagokat.

Az alábbi kép egy példa a diffrakcióra egy kör alakú szerkezeten, éles határ nélkül. A keréken szinuszos intenzitáscsökkenés esetén nem következik be magasabb rendű diffrakció (lásd még a zónalapot ).

Kép periodikus struktúrákkal

A bal oldali képen az Indiai -óceán SAR -képe látható , különböző hullámhosszúságú vízhullámokkal. A jobb felső sarokban lévő belső hullámok hullámhossza körülbelül 500 m. A szél által keltett felületi hullámok nem láthatók a csökkentett ábrázolásban. A számított diffrakciós mintázatban a két sötét visszaverődés (lásd a rövid nyilat) jelzi a szabályos hosszú periódusú vízhullámok irányát és átlagos hullámhosszát is. A felszíni hullámok hullámhossza jobban változik, ezért nem nyújtanak éles visszaverődést. A hullámterjedésnek két kiváló iránya van, amelyek csak a közvetlen képen láthatók. A hullámhossz körülbelül 150 m (hosszú nyíl) és 160 m (kissé rövidebb nyíl).

Matematikai alap

A diszkrét Fourier -transzformációban megjelenő komplex számok

${\ displaystyle \ mathrm {e} ^ {\ mathrm {i} \, 2 \ pi {\ frac {n} {N}}}}$

vannak -edik gyökerei egység , d. vagyis megoldások az egyenletre . Legyen a „legkisebb”, azaz primitív gyökér az első negyedben. Ez kielégíti az egységgyökerek geometriai összegeinek alábbi azonosságát ${\ displaystyle N}$${\ displaystyle q ^ {N} = 1}$${\ displaystyle q: = \ mathrm {e} ^ {2 \ pi \, i / N}}$

${\ displaystyle \ displaystyle \ sum _ {k = 0} ^ {N-1} q ^ {nk} = N \ delta _ {0, n}}$ val vel ${\ displaystyle n = 0, \ dotsc, N-1}$

mert az . ${\ displaystyle \ displaystyle \ sum _ {k = 0} ^ {N-1} x ^ {k} = {\ frac {x ^ {N} -1} {x-1}}}$${\ displaystyle x \ neq 1}$

Ez az a "mély ok", amiért az inverz DFT működik.

Definiáljuk a vektorokban ${\ displaystyle \ mathbb {C} ^ {N}}$

${\ displaystyle f_ {n}: = (\ mathrm {e} ^ {\ mathrm {i} 2 \ pi {\ frac {nk} {N}}}) _ {k = 0, \ pöttyök, N-1} }$ számára ${\ displaystyle n = 0, \ dotsc, N-1,}$

tehát ortonormális alapot képeznek a skaláris termékhez

${\ displaystyle \ langle x, y \ rangle = {\ frac {1} {N}} \ sum _ {k = 0} ^ {N-1} x_ {k} {\ bar {y}} _ {k} }$.

Ez vonatkozik

${\ displaystyle \ langle f_ {n}, f_ {m} \ rangle = {\ frac {1} {N}} \ sum _ {k = 0} ^ {N-1} \ mathrm {e} ^ {\ mathrm {i} 2 \ pi {\ frac {(nm) k} {N}}} = \ delta _ {n, m} = {\ begin {case} 1 & n = m \\ 0 & n \ neq m \ vége {esetek}}}$.

Minden vektor ábrázolható ortonormális alapon: ${\ displaystyle x = (x_ {0}, \ dotsc, x_ {N-1}) \ in \ mathbb {C} ^ {N}}$

${\ displaystyle \ displaystyle x = \ összeg _ {n = 0} ^ {N-1} \ langle x, f_ {n} \ rangle \ cdot f_ {n}}$.

Az együtthatókat Fourier -együtthatóknak nevezik (általában minden ortonormális rendszer esetében is) , így a DFT a Fourier -együtthatók vektorát az additív állandó kivételével egy vektorhoz rendeli . ${\ displaystyle \ langle x, f_ {n} \ rangle}$${\ displaystyle x}$${\ displaystyle X = \ operatornév {DFT} (x)}$

Ha más vektorral , akkor a Fourier -együttható Parseval -egyenlete érvényes : ${\ displaystyle Y = \ operatornév {DFT} (y)}$${\ displaystyle y = (y_ {0}, \ dotsc, y_ {N-1}) \ in \ mathbb {C} ^ {N}}$

${\ displaystyle \ langle x, y \ rangle = \ sum _ {n = 0} ^ {N-1} \ langle x, f_ {n} \ rangle \ langle f_ {n}, y \ rangle = \ sum _ { n = 0} ^ {N-1} X_ {n} {\ bar {Y}} _ {n}}$.

A DFT értelmezései

A Fourier -transzformáció diszkretizálása

A Fourier -transzformáció lehetővé teszi olyan funkciók gondolkodását, amelyek valódi érvekkel (és különféle korlátozásokkal, például: integrálhatóság , periodicitás vagy bomlás a végtelenben) rezgésekből állnak:

${\ displaystyle f (t) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {- \ infty} ^ {\ infty} {\ hat {f}} (\ omega) \ mathrm {e} ^ {\ mathrm {i} \ omega t} \, \ mathrm {d} \ omega}$

A Fourier -elmélet fontos megállapítása, hogy az amplitúdót hasonló módon lehet meghatározni ${\ displaystyle {\ hat {f}} (\ omega)}$

${\ displaystyle {\ hat {f}} (\ omega) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {- \ infty} ^ {\ infty} f (t) \ mathrm {e} ^ {- \ mathrm {i} \ omega t} \, \ mathrm {d} t.}$

Ha olyan nagy sugarat választunk, hogy a jelentéktelen része csak az intervallumon kívülre esik , akkor az is folytonos, és olyan nagy számot választunk, hogy elég kicsi ahhoz, hogy értelmesen egyes legyen, azaz H. függvényértékek segítségével a transzformációs képletben szereplő Fourier -integrált értelemszerűen le lehet cserélni egy összeggel: ${\ displaystyle R}$${\ displaystyle [-R, R]}$${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle N}$${\ displaystyle T: = R / N}$${\ displaystyle f}$${\ displaystyle f (kT)}$

${\ displaystyle {\ hat {f}} (\ omega) \ kb F (\ omega) = {\ frac {1} {\ sqrt {2 \ pi}}} \ sum _ {k = -N} ^ {N } \ mathrm {e} ^ {- \ mathrm {i} \ omega kT} f (kT) \, T}$

Az állandó tényező kivételével ez megfelel a DFT számítási képletnek. A vektor rendelkezik elemekkel. Azt már tudjuk, hogy ez elegendő, a frekvencia-együtthatók a frekvenciákat , hogy meghatározza a függvény értéke a vektor rekonstruálni. Az iDFT állandóinak szükséges adaptációjával megkapjuk ${\ displaystyle T / {\ sqrt {2 \ pi}}}$${\ displaystyle x = (f (-NT), \ dotsc, f (NT))}$${\ displaystyle 2N + 1}$${\ displaystyle 2N + 1}$${\ displaystyle \ omega _ {n}: = 2 \ pi \ cdot {\ frac {n} {(2N + 1) T}}}$${\ displaystyle n = -N, \ dotc, -1,0,1, \ dotc, N}$${\ displaystyle x}$

${\ displaystyle f (nT) = {\ frac {1} {\ sqrt {2 \ pi}}} \ sum _ {k = -N} ^ {N} \ mathrm {e} ^ {\ mathrm {i} \ omega _ {k} nT} F (\ omega _ {k}) \, {\ frac {2 \ pi} {(2N + 1) T}}.}$

A frekvenciatartományban lévő diszkretizációs távolság arányos , azaz az előfeltétel szerint is kicsi, így ez a számítás megfelel az inverz Fourier -transzformáció diszkretizálásának. ${\ displaystyle 1 / R}$

A Fourier -transzformációról a DFT -re való átmenet során a következő változásokat kell észrevenni:

• A jel diszkrét , egyenlő távolságra lévő időpontokban érhető el ( két egymást követő időpont közötti távolság), ez az egyik ilyen időpont.${\ displaystyle T =}$${\ displaystyle 0}$
• A jel véges hosszúságú ( értékek száma), amelyeket nagy intervallumon belül értékként értelmezünk .${\ displaystyle 2N + 1 =}$${\ displaystyle [-NT, NT]}$
• A Fourier -együttható kiszámításának integráljai a DFT -ben összegekké válnak.
• A spektrumot csak véges számú (körkörös) frekvenciára számítjuk ki , amelyek frekvenciája periodikus , és az időszak nagyon nagy a feltételezés szerint ( kicsi).${\ displaystyle \ omega = 2 \ pi n / ((2N + 1) T)}$${\ displaystyle n = -N, \ dotc, -1,0,1,2, \ dotc, N}$${\ displaystyle 2 \ pi / T}$${\ displaystyle T}$

Fourier -sorozat diszkretizálása

Minden periodikus függvény valódi argumentummal (és ismét korlátozásokkal, mint például: integrálhatóság, pólusok nélkül) és periódus funkciók sorozataként ábrázolható olyan szinuszokkal, amelyek törtrészei (ún. Fourier-sorozat ): ${\ displaystyle L}$${\ displaystyle L}$

${\ displaystyle f (t) = \ sum _ {n \ in \ mathbb {Z}} c_ {n} (f) \ mathrm {e} ^ {\ mathrm {i} \ cdot \ omega _ {n} t} }$ val vel ${\ displaystyle \ omega _ {n} = {\ frac {2 \ pi n} {L}}}$

Ha megszakítjuk a sorozat bővítését nagy határokon felül és lent , akkor a${\ displaystyle 1-M}$${\ displaystyle NM}$${\ displaystyle T: = L / N}$

${\ displaystyle f (t_ {k}) = f (kT) \ kb \ sum _ {n = 1-M} ^ {NM} c_ {n} (f) \ mathrm {e} ^ {2 \ pi \ mathrm {i} \ cdot {\ frac {nk} {N}}},}$

d. vagyis valamilyen inverz DFT -t kapunk. Ez azt jelenti, hogy az együtthatók megközelíthetők a DFT használatával

${\ displaystyle c_ {n} (f) \ kb {\ frac {1} {L}} \ sum _ {k = 0} ^ {N-1} f (kT) \ mathrm {e} ^ {- \ mathrm {i} \ cdot {\ frac {2 \ pi nk} {N}}} \ cdot {\ frac {L} {N}} = {\ frac {1} {L}} \ sum _ {k = 0} ^ {N-1} f (t_ {k}) \ mathrm {e} ^ {- \ mathrm {i} \ cdot {\ frac {2 \ pi n} {L}} t_ {k}} \ cdot T. }$

A végtelenül nagy határok között a Fourier -sorozat ismert együtthatói integrálja: ${\ displaystyle N}$

${\ displaystyle c_ {n} (f) = {\ frac {1} {L}} \ int _ {0} ^ {L} f (t) \ mathrm {e} ^ {- \ mathrm {i} \ cdot {\ frac {2 \ pi n} {L}} t} \, \ mathrm {d} t}$

tulajdonságait

Mintavett függvények spektruma

A diszkrét Fourier -transzformáció periodikus spektrummal rendelkezik, megismétlődik a mintavételi frekvenciával, és szimmetrikus a mintavételi frekvenciával. A következők érvényesek:

${\ displaystyle F \ left (\ omega + {\ frac {2 \ pi} {T}} m \ right) = C \ sum _ {k = 0} ^ {N-1} f (kT) \ mathrm {e } ^ {- \ mathrm {i} \ omega kT} \ mathrm {e} ^ {- \ mathrm {i} {\ frac {2 \ pi} {T}} mkT} = F (\ omega)}$(mert a természetes számok , és )${\ displaystyle \ mathrm {e} ^ {- \ mathrm {i} 2 \ pi mk} = 1}$${\ displaystyle m}$${\ displaystyle k}$

${\ displaystyle F \ bal ({\ frac {2 \ pi} {T}} - \ omega \ right) = C \ sum _ {k = 0} ^ {N -1} f (kT) \ mathrm {e} ^ {- \ mathrm {i} {\ frac {2 \ pi} {T}} kT} \ mathrm {e} ^ {+ \ mathrm {i} \ omega kT} = F ^ {*} (\ omega)}$

Ha a mintavételezett jel a mintavételi frekvencia felénél magasabb frekvenciakomponenseket tartalmaz, akkor az eredeti jel spektruma átfedésben van a mintavételi frekvencián tükröződő jelkomponensekkel, és alias hatás lép fel.

Alias ​​hatás

Általában az idődiszkrét jel egy folyamatos jel diszkretizálásával jön létre . A DFT -ből származó spektrumok csak akkor azonosak a mögöttes folyamatos jel spektrumával, ha a mintavételi tétel nem sérült a mintavétel során . Az alapsávban lévő jelek esetében a mintavételi frekvenciának több mint kétszer akkoranak kell lennie, mint a maximális előforduló frekvencia ( Nyquist frekvencia ). Ha a mintavételi tételt megsértik, az eredeti jel meghamisításra kerül (aliasing az időtartományban). Az anti-aliasing egyik lehetősége az , hogy a hatást elkerülve korlátozza a jelet a rendszer bemenetén.

Időben korlátozott függvény DFT

Periodikus függvények esetén (a folyamatos Fourier -transzformációval analóg módon ) egy 1 / periódushosszú frekvenciasávú vonalspektrumot kapunk.

Egy időre korlátozott diszkrét függvény egy periodikus diszkrét függvényből származtatható, ha pontosan egy periódust vág ki egy időablakból : ${\ displaystyle g (kT)}$${\ displaystyle f (kT)}$${\ displaystyle w (t)}$

${\ displaystyle g (kT) = f (kT) \ cdot w (t)}$

Mivel a Fourier-transzformációban az időtartományban lévő függvények szorzata megfelel a Fourier-transzformáció konvolúciójának a frekvenciatartományban, az időkorlátozott függvény DFT-je a periodikus függvény DFT-jének és a Fourier-transzformációnak a konvolúciójából adódik . az időablak : ${\ displaystyle G (\ omega)}$${\ displaystyle F (\ omega)}$${\ displaystyle W (\ omega)}$

${\ displaystyle G (\ omega) = F (\ omega) \ star W (\ omega)}$

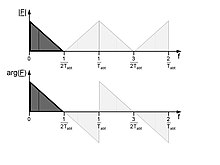
Az eredmény egy vonalspektrum, amelyet elken az időablak Fourier -transzformációja . Az időablak hatása a periodikus függvény DFT -jére (vastag vonalak) szaggatott vonallal látható a 3. ábrán. Az időkorlát frekvenciaösszetevőket ad hozzá az elemzett frekvenciavonalakhoz.

A periodikus függvényről az időkorlátozott funkcióra való áttérés miatt a spektrum meghatározására szolgáló számítási módszert nem kell megváltoztatni. Továbbá a diszkrét frekvenciavonalakat úgy számítják ki, mintha periodikus függvény lenne mögöttük. Az időablak hatására minden számított frekvenciavonal egy teljes frekvenciatartományt reprezentál, nevezetesen azt a frekvenciatartományt, amelyet az időablak Fourier -transzformációja adott hozzá. Ezt a viselkedést szivárgáshatásnak is nevezik .

Szivárgási hatás

A jel időkorlátja miatt a bemeneti jel megszakadhat. A csonka bemeneti jel csak akkor alakítható át helyesen a DFT -vel, ha rendszeresen folytatható. Ha a jelet nem lehet periodikusan folytatni, olyan frekvenciákat tartalmaz, amelyek nem tartoznak a DFT által kiszámított diszkrét frekvenciákhoz. A DFT ezeket a frekvenciákat "közelíti" a szomszédos frekvenciákon keresztül, és az energia ezekre a frekvenciákra oszlik el. Ezt szivárgáshatásnak nevezik .

Az időkorlát egyenértékű egy téglalap alakú függvényű szorzással, és megfelel a frekvenciatartomány si funkciójával való konvolúciónak . Ez egy másik módja a szivárgási hatás vizsgálatának. Természetesen ez vonatkozik más ablakfunkciókra is (pl. Hamming, von Hann, Gauss). Az ablakfunkció spektruma (vagy a spektrum szélessége) ezért döntő a szivárgás szempontjából. Az amplitúdó pontossága az ablakfüggvény másik kritériuma.

Csúszó DFT sávszűrő bankként

Az időkorlátozott funkció DFT-je sávszűrő banknak is tekinthető.

• Ezeknek a sávszűrőknek a középfrekvenciái megfelelnek annak a funkciónak a frekvenciavonalaihoz, amely akkor következik be, amikor a megfigyelt időszakasz periodikusan megismétlődik (1 / ablak szélessége többszöröse).
• A sávszűrő szélességét és meredekségét az időablak Fourier -transzformációja határozza meg (lásd 3. ábra).

A sávszűrő tulajdonságai megváltoztathatók a megfelelő időablak -funkció kiválasztásával.

• Egy téglalap alakú időablak esetén, amelynek megszakítási pontjai vannak az ablakhatáron, a sávszűrő átviteli tartományán kívül eső frekvenciákat 1 / frekvenciával csillapítják; 6 dB / oktáv lejtést érnek el (lásd 2. ábra).
• Ha az ablak funkció folyamatos, a sávszűrő átviteli tartományán kívül eső frekvenciákat 1 / frekvencia ² gyengíti; 12 dB / oktáv meredekség érhető el.
• Ha az ablakfüggvény 1. deriváltja folyamatos, akkor a sávszűrő átviteli tartományán kívül eső frekvenciákat 1 / ^3. frekvenciával csillapítják; a meredekség 18 dB / oktáv.
• stb.

Ha az egymást követő időszegmensek Fourier -transzformációját meghatározzuk, a csúszó Fourier -transzformációt kapjuk. Egy új időszegmens elemzésével ezután új mintaértékeket kapunk a spektrális vonalak időbeli lefolyására (vagyis a "sávszűrő" kimenetein lévő jelek időbeli lefolyására).

A csúszó DFT bizonytalansági összefüggése

A csúszó DFT idő- és frekvenciafelbontása nem választható ki egymástól függetlenül.

• Ha nagyfrekvenciás felbontású jeleket szeretne elemezni, akkor nagyon nagyra kell növelnie az időablakot, alacsony időfelbontást kap.
• Ha nagy időfelbontásra van szüksége, akkor nagyon rövidre kell állítania az időablak szélességét, de akkor csak néhány frekvenciavonalat határozhat meg.
• A következők érvényesek: Frekvenciafelbontás ≈ 1 / időablak szélessége (ha 1 kHz frekvenciafelbontásra van szükség, akkor az időablaknak legalább 1 ms hosszúnak kell lennie).

FFT

A 2 -es teljesítményként ábrázolható blokkhosszak esetén a számítást a gyors Fourier -transzformációs (FFT) algoritmus segítségével lehet elvégezni . Általánosságban: Ha a blokk hosszát figyelembe lehet venni, akkor a hosszúság DFT -jét a hosszúságú DFT -k és két egyszerű mátrix szorzatára bontjuk . ${\ displaystyle N}$${\ displaystyle N = KM}$${\ displaystyle N}$${\ displaystyle K}$${\ displaystyle M}$

Goertzel algoritmus

A Goertzel -algoritmus bármely blokkhosszra és egyetlen vagy néhány spektrális komponens meghatározására is használható . Az előny egy nagyon hatékony megvalósítás a számítógépes rendszerekben, mivel az egyes spektrális komponensek számítása csak egy komplex szorzást és két komplex összeadást tartalmaz. ${\ displaystyle N}$

Alkalmazások

• Egy jel Fourier -transzformációjának kiszámítása
• Jel elemzés
• Rezgésanalízis és modális elemzés
• A jelek feldolgozása
• Korrelációk kiszámítása
• Polinomiális szorzatok kiszámítása ${\ displaystyle {\ mathcal {O}} (n \ cdot \ log (n))}$

A felszíni akusztikus hullámszűrők (SAW szűrők = = = SAW szűrőfelszíni akusztikus hullámszűrők) kiszámításához az inverz Fourier -transzformáció a szükséges átviteli függvény (az impulzusválasz -csoportot képviseli ). Ezt a feladatot számítógépek végzik.

Lásd még

• összecsukható
• Gábor átalakítása
• Laplace -transzformáció
• z átalakítás
• Diszkrét koszinusz transzformáció
• Wavelet transzformáció
• Ablak funkció
• Fourier sorozat
• Rövid idejű Fourier-transzformáció

irodalom

• Tilman Butz: Fourier -transzformáció a gyalogosok számára. 7. kiadás. Vieweg + Teubner Verlag, Wiesbaden 2011, ISBN 978-3-8348-0946-9 , 4. fejezet.
• MW Wong: Diszkrét Fourier -elemzés. Birkhäuser Verlag, Bázel 2011, ISBN 978-3-0348-0115-7 .