Háromszög alakú arc

általános háromszög

A háromszög területének pontos kiszámítása az egyik legrégebbi probléma a geometriában . Már az ókori Egyiptomban, amikor a nílusi áradások visszahúzódtak, újra kellett osztani a termékeny termőföldet. A háromszögek és területszámításuk ma is fontos alapot jelentenek a földméréshez - a szabálytalan területeket háromszögeléssel lehet meghatározni. A háromszög alakú hálózatok elvét a matematika modern területein is alkalmazzák .

A fizikai egység van a négyzetméter (m²).

Területszámítás egy lapos háromszögre

A háromszög területeit könnyű kiszámítani, ha ismeri mind a három oldal hosszát, vagy a két oldal hosszát és az azokba foglalt szöget.

Tekintettel mindhárom oldalhosszra

Ha egy háromszög mindhárom oldalhossza ismert, akkor Heron tétele alkalmazható:

${\ displaystyle F = {\ sqrt {s (sa) (sb) (sc)}}}$

Ez a háromszög kerülete fele . ${\ displaystyle s = {\ tfrac {a + b + c} {2}}}$

Egyenlő oldalú háromszög speciális esete

Innen következik a fél kerület . Ennek beillesztése a fenti képletbe a következőket eredményezi: ${\ displaystyle a = b = c}$${\ displaystyle s = {\ tfrac {3a} {2}}}$

${\ displaystyle F = {\ sqrt {{\ tfrac {3a} {2}} ({\ tfrac {a} {2}}) ({\ tfrac {a} {2}}) ({\ tfrac {a} {2}})}} = {\ tfrac {\ sqrt {3}} {4}} a ^ {2}}$

Adott két oldalhossz és a szögek

A háromszög és a paralelogramma kapcsolata .

Ha egy háromszög két oldalhossza (és a hozzá tartozó szög ) ismert, akkor a háromszög területe többféle módon meghatározható. A háromszög területének általános képlete az ${\ displaystyle F}$

${\ displaystyle F = {\ frac {a \ cdot h} {2}},}$

ez az alapoldal és az azt követő háromszög függőleges álló magassága . A képlet adja meg a paralelogramma tartalmának felét , mert minden háromszöget ki lehet egészíteni egy önmagának egy elforgatott másolatával, hogy a megfelelő paralelogramma legyen. Felülete nyírással téglalapra csökkenthető . Egy másik megközelítés azért merül fel, mert egy háromszöget mindig egy trapéz speciális esetének tekinthetünk , amelyben a második alap csak egy pontból áll. ${\ displaystyle a}$${\ displaystyle h}$

Noha a háromszög mindkét oldala alapoldalként használható, a megfelelő magasság kiszámítása azonban kivételes esetek kivételével geometriai szempontból lehetetlen. A trigonometria egy következtetést vonja le: . Ennek eredményeként: ${\ displaystyle h \, (= h_ {a}) = b \ cdot \ sin {\ gamma}}$

${\ displaystyle F = {\ frac {ab \ cdot \ sin {\ gamma}} {2}}.}$

Különleges esetek

Derékszögű háromszög

Abban az esetben, derékszögű háromszögek , a magassága egybeesik az egyik cathets .

A derékszögű háromszögek esetében a magasságot nem kell külön kiszámítani. Ha a két katéter hossza ismert, az eredményt ad . ${\ displaystyle F = {\ tfrac {a \ cdot b} {2}}}$

Egyenlő szárú háromszög

A magassága egy egyenlő szárú háromszög a lábak mindig elvágja a bázis közepén, és ezért kell kiszámítani a Pitagorasz-tétel , és ezért ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle h = {\ sqrt {a ^ {2} - {\ tfrac {b ^ {2}} {4}}}}}$

${\ displaystyle F = {\ tfrac {b} {4}} {\ sqrt {4a ^ {2} -b ^ {2}}}}$.

A fentiekből A képlet eredményei:

${\ displaystyle F = {\ frac {1} {2}} {a ^ {2}} \ cdot \ sin {\ gamma}.}$

Egyenlő oldalú háromszög

Ennek szabályos sokszög minden oldalú háromszög a élhosszúságú van a magasságot , ahonnan a terület eredmények . ${\ displaystyle a}$${\ displaystyle h = {\ tfrac {a {\ sqrt {3}}} {2}}}$${\ displaystyle F = {\ tfrac {\ sqrt {3}} {4}} a ^ {2}}$

Mivel az egyenlő oldalú háromszög szögei mind azonos méretűek, a fentiekből következik. Képlet is:

${\ displaystyle F = {\ frac {1} {2}} {a ^ {2}} \ cdot \ sin 60 ^ {\ circ}.}$

Egyéb esetek

Ha a háromszög egyértelműen azonosítható , további szögeket vagy oldalhosszakat kell kiszámítani, amíg elegendő információ nem áll rendelkezésre a fenti képletek egyikéhez.

Számítás koordinátákkal

A síkban

A háromszög alakú terület levezetése trapéz segítségével ${\ displaystyle F = A_ {1} + A_ {2} -A_ {3}}$

Háromszög alakú területet számítottunk az oldalsó vektorai által lefedett párhuzamosan. ${\ displaystyle F = {\ tfrac {1} {2}} balra | \ det \ balra ({\ begin {matrix} u_ {x} & v_ {x} \\ u_ {y} & v_ {y} \ end { mátrix}} \ right) \ right |}$ ${\ displaystyle = {\ tfrac {1} {2}} | u_ {x} v_ {y} -u_ {y} v_ {x} |}$

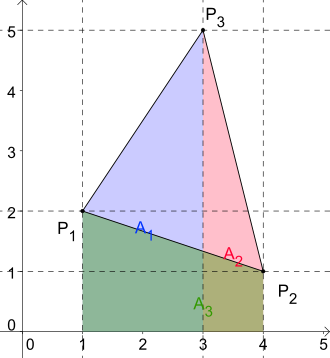
Az euklideszi sík a koordináta tengelyeket , a környéken egy háromszög pontot , és lehet származnak a trapéz formula . A háromszög (esetleg az első kvadránsra tolva) vetülete az egyik tengelyre három trapézot eredményez, amelyek összege vagy különbsége a háromszög alakú terület. Az összes szükséges paraméter kiolvasható a koordinátákból. A háromszög területére kapjuk: ${\ displaystyle P_ {1} = (x_ {1}, y_ {1})}$${\ displaystyle P_ {2} = (x_ {2}, y_ {2})}$${\ displaystyle P_ {3} = (x_ {3}, y_ {3})}$

${\ displaystyle F = {\ tfrac {1} {2}} (y_ {3} + y_ {1}) (x_ {3} -x_ {1}) + {\ tfrac {1} {2}} (y_ {2} + y_ {3}) (x_ {2} -x_ {3}) - {\ tfrac {1} {2}} (y_ {2} + y_ {1}) (x_ {2} -x_ { 1})}$

${\ displaystyle = {\ tfrac {1} {2}} (x_ {1} (y_ {2} -y_ {3}) + x_ {2} (y_ {3} -y_ {1}) + x_ {3 } (y_ {1} -y_ {2}))}$

Ez a képlet nagyon egyértelműen ábrázolható egy meghatározó segítségével :

${\ displaystyle F = {\ frac {1} {2}} \ left | \ det \ left ({\ begin {mátrix} 1 & x_ {1} & y_ {1} \\ 1 & x_ {2} & y_ {2} \\ 1 & x_ {3} & y_ {3} \ end {mátrix}} \ right) \ right | = {\ frac {1} {2}} \ bal | \ det \ bal ({\ begin {mátrix} 1 & 1 & 1 \\ x_ {1 } & x_ {2} & x_ {3} \\ y_ {1} & y_ {2} & y_ {3} \ end {mátrix}} \ right) \ right |}$

Ha valaki eltolja a háromszöget úgy, hogy az a nulla pontra essen , akkor Laplace fejlõdési tételének (az elsõ oszlop szerinti fejlõdés) alapján az eredmény : ${\ displaystyle P_ {1}}$

${\ displaystyle {\ begin {aligned} F & = {\ frac {1} {2}} \ left | \ det \ left ({\ begin {mátrix} 1 & 1 & 1 \\ 0 & x_ {2} -x_ {1} & x_ {3 } -x_ {1} \\ 0 & y_ {2} -y_ {1} & y_ {3} -y_ {1} \ end {mátrix}} \ right) \ right | \\ & = {\ frac {1} {2 }} \ left | \ det \ left ({\ begin {matrix} x_ {2} -x_ {1} & x_ {3} -x_ {1} \\ y_ {2} -y_ {1} & y_ {3} - y_ {1} \ end {mátrix}} \ right) \ right | \\ & = {\ frac {1} {2}} | (x_ {2} -x_ {1}) (y_ {3} -y_ { 1}) - (x_ {3} -x_ {1}) (y_ {2} -y_ {1}) | \ end {igazítva}}}$

Ez a második, determináns formában megjelenített kép a párhuzamos oldalúak térfogatának általános képletéből is származik , mivel a kétdimenziós párhuzamos egy paralelogramma, amelynek kétszerese a háromszög területe. Ezért szükséges, hogy az a - Matrix determinánsának mennyisége, amelynek oszlopai egy háromszög oldalirányú vektorai, a kettős terület adja meg ezt a háromszöget. Ugyanezt a megközelítést kapunk, ha a háromszög alakú terület nem tisztázott összegeként trapéz-nak, de az összeg a három integrálok át a lineáris függvények , amelyek meghatározzák a három oldalról. ${\ displaystyle 2 \ szor 2}$

A három oldalt görbékként is ábrázolhatjuk a síkban, majd a háromszög darabonként sima zárt görbét képez, amelynek zárt területe a Leibniz-szektor képletével kiszámítható.

Háromdimenziós térben

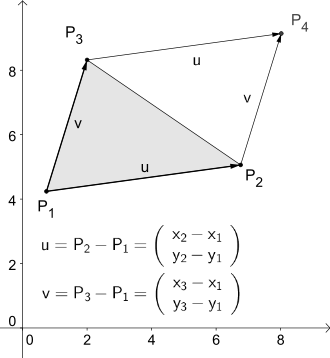
Az euklideszi tér a háromszög területe, amely által kifeszített , és kapjuk a segítségével a kereszt termék a két vektor és a . Ez azt eredményezi, vektor, amelynek euklideszi normája egyenlő a terület a paralelogramma által kifeszített és . ${\ displaystyle (0,0,0), (x_ {1}, x_ {2}, x_ {3})}$${\ displaystyle (y_ {1}, y_ {2}, y_ {3})}$${\ displaystyle {\ vec {x}} = (x_ {1}, x_ {2}, x_ {3})}$${\ displaystyle {\ vec {y}} = (y_ {1}, y_ {2}, y_ {3})}$${\ displaystyle {\ vec {x}}}$${\ displaystyle {\ vec {y}}}$

${\ displaystyle 2F = \ left | {\ vec {x}} \ times {\ vec {y}} \ right | = \ left | {\ begin {pmatrix} x_ {1} \\ x_ {2} \\ x_ {3} \ end {pmatrix}} \ times {\ begin {pmatrix} y_ {1} \\ y_ {2} \\ y_ {3} \ end {pmatrix}} \ right | = \ left | {\ begin { pmatrix} x_ {2} y_ {3} -x_ {3} y_ {2} \\ x_ {3} y_ {1} -x_ {1} y_ {3} \\ x_ {1} y_ {2} -x_ {2} y_ {1} \ end {pmatrix}} \ right | = {\ sqrt {(x_ {2} y_ {3} -x_ {3} y_ {2}) ^ {2} + (x_ {3} y_ {1} -x_ {1} y_ {3}) ^ {2} + (x_ {1} y_ {2} -x_ {2} y_ {1}) ^ {2}}} \,.}$

Vagy: A skaláris szorzat segítségével

${\ displaystyle 2F = {\ sqrt {{\ vec {x}} ^ {2} {\ vec {y}} ^ {2} - ({\ vec {x}} \ cdot {\ vec {y}}) ^ {2}}}}$.

Terület kiszámítása szférikus háromszögek

Szigorúan véve: egyetlen háromszög sem sík a föld felszínén , mivel a földről ismert, hogy megközelítőleg gömb alakú (lásd a föld görbületét ). Nagyon nagy háromszögek esetén (pl. Fokváros - Rio de Janeiro - Tokió) ezért a gömb alakú geometria (vagy a gömb trigonometria) vagy a differenciálszámítás módszereihez kell folyamodni:

Szerint a Legendre-tétel , egy kis gömb alakú háromszög szinte ugyanazon a területen, mint egy lapos háromszög három oldala egyenlő hosszúságú. Ez az úgynevezett szintezés annál pontosabb lesz, minél kisebbek a háromszögek. Ennek eredményeként a gömb alakú háromszög területének kiszámításához iteratív módszer jön létre: A háromszög határát képező geodéziai vonalakat felezzük meg ismételten, és számítsuk ki a kisebb háromszögekből származó területösszegeket. Ennek a folyamatnak a határa létezik, és ez a gömb alakú háromszög területe.

Természetesen két közvetlen út vezet a cél gyorsabban: vagy via megfelelő képletek gömbháromszögtan keresztül vagy a gömb alakú felesleges (a többlet a szögek összege 180 °). Gömb alakú háromszög belső szögeivel , amely egy sugarú gömbön fekszik, a következő képlet érvényes: ${\ displaystyle \ alfa, \ béta, \ gamma}$${\ displaystyle r}$

${\ displaystyle F = (\ alpha + \ beta + \ gamma - \ pi) \ cdot r ^ {2}}$

A felesleg egyenesen arányos a háromszög területével, amely elég pontos a föld ellipszoidján a geodézia gyakorlásához . A gömb alakú háromszögek cseréje lapos egyenértékükkel 10 km-es távolságból túl pontatlanná válik.

irodalom

• Martin Nitschke: Geometria . Hanser Verlag, ISBN 3-446-22676-1 .

web Linkek

• Eric W. Weisstein : háromszög alakú terület . In: MathWorld (angol).