Szimmetria (geometria)

Szimmetria és aszimmetria

szimmetria

az építészetben

a biológiában

Leonardo da Vinci " Vitruviánus embere "

A szimmetria geometriai kifejezés ( ókori görög συμμετρία szimmetria egyenletesség, egyenletesség , σύν syn "együtt" és μέτρον metron , mérték) azt a tulajdonságot jelöli, hogy egy geometriai objektum mozgásokon keresztül leképezhető önmagára , azaz változatlannak tűnik. Egy olyan transzformációt, amely egy objektumot saját magára képez le, szimmetrialeképezésnek vagy szimmetriaműveletnek nevezzük .

Néha két (vagy több) különböző geometriai tárgyat szimmetrikusnak mondanak egymással, ha együtt nézve szimmetrikus alakot alkotnak.

A figyelembe vett méretek számától függően a következő szimmetriák léteznek:

Szimmetriák az egydimenziósban

Az egydimenziós, azaz egyenes vonalban van a szimmetria egyetlen pont vonatkozásában, valamint a fordítás szimmetriája (elmozdulás).

Szimmetria két dimenzióban

Kétdimenziós esetén különbséget kell tenni a pont- és tengelyszimmetria között . Ezenkívül itt is előfordulnak transzlációs szimmetriák.

Forgásszimmetria / forgási szimmetria

Négy szabályos sokszög és két további geometriai alakzat a forgási szimmetriájuk kulcsfiguráival, más néven forgási szimmetriával ( n = 1 azt jelenti: forgásszimmetria nélkül)

A kétdimenziós geometriai alaknak ezután az a tulajdonsága, hogy forgásszimmetrikus, ha az ábrának van egy központi pontja, és az ábra önmagára lesz leképezve, amikor elforgatja ezt a pontot. Egy kör vagy körgyűrű forgásszimmetrikus szűkebb értelemben. Bármely szögben történő elforgatás önmagára térképezi.

Az ábrát forgásszimmetrikusnak is nevezzük, ha önmagán ábrázolható úgy, hogy a középpont körül rögzített szögben elforgatja 0 ° << 360 ° -kal. A forgásszög csak úgy határozható meg, ha a teljes szöget elosztjuk egy > 1 értékkel , azaz . Ez a szám a forgási szimmetria mértékegysége, és "számnak" is nevezik. Ennek megfelelően ezt a szimmetriát -számos vagy -szeres forgási szimmetriának is nevezik (analóg az angol " -szeres forgási szimmetria" -val ) vagy " -számos forgási szimmetria" -nak is.${\ displaystyle \ varphi}$${\ displaystyle \ varphi}$${\ displaystyle n}$${\ displaystyle \ varphi = {\ tfrac {360 ^ {\ circ}} {n}}}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$

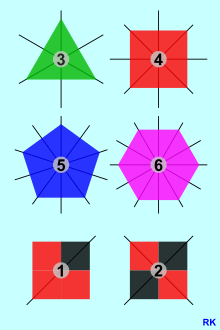
A szabályos sokszögek tipikus forgásszimmetrikus alakok. A jobb oldali grafikon az első négyet mutatja, és a forgási szimmetria lehető legnagyobb kulcsfigurája is be van húzva. Ezenkívül két további ábra látható, nevezetesen egy anélkül és egy kettős forgásszimmetriával. A triviális esetben nincs forgási szimmetria / forgási szimmetria, és az 1 -es kódszámot nem használják matematikai kontextusban, kivéve, ha azonosítani szeretné a triviális ciklikus csoportot , amely csak az azonos leképezésből áll . ${\ displaystyle n}$${\ displaystyle n = 1}$ ${\ displaystyle C_ {1}}$

A Schoenflies szimbólum meghatározza a forgási szimmetria szimmetria elemeinek és szimmetriacsoportjainak szimbólumát . További példák a kettős forgásszimmetriák a pont-szimmetrikus számok alább látható . Az a tény, hogy a pontszimmetrikus tárgyak mindig forgásszimmetrikusak, azonban csak a kétdimenziósra érvényesek. ${\ displaystyle C_ {n}}$

Tükörszimmetria / tengelyszimmetria

Szimmetrikus tárgyak tükrözése a síkban

A fenti sokszögek összes szimmetriaeleme, beleértve a tükörszimmetria vonalaikat is

A tükörszimmetria a szimmetria egyik formája, amely akkor fordul elő, amikor a szimmetriatengelyre merőleges tárgyak tükröződnek (lásd rajz). Kétdimenziós értelemben az axiális szimmetria vagy tengelyszimmetria szinonimája . A következő minden tengelytükrözésre vonatkozik:

1. Az ábra és a kép egybevág egymással.
2. A vonal és a képsor azonos hosszúságú.
3. A látószög és a látószög ugyanaz.
4. Az ábra és az ábrás ábra különböző forgásirányokkal rendelkezik, feltéve, hogy az ábrán a forgásérzék van meghatározva.

Példák

• A háromszögeknek egy vagy három tükörszimmetriatengelyük lehet: Az egyenlő szárú háromszög tengelyszimmetrikus az alap merőlegesével. A homogén egyenlő oldalú háromszögeknek három tükörszimmetriatengelyük van, amint azt a szemközti grafika is mutatja. Az a tény, hogy ezekben a színes sokszögekben a szimmetriatengelyek száma megegyezik a forgási szimmetria fent említett számával, általában nem érvényes, mivel sok forgásszimmetrikus objektum nem rendelkezik tükörszimmetriával, például a pont -szimmetrikus formák az alábbiakban láthatók .
• A négyszögek egy, kettő vagy akár négy tükörszimmetriatengelyt is tartalmazhatnak:
  • Legalább az egyik tükörszimmetriatengely egyenlő szárú trapézokat tartalmaz (a párhuzamos oldalak középpontjain keresztül) és sárkány négyzeteket (átló mentén).
  • Legalább két tükörszimmetriatengely van a téglalapra (a szemközti oldalakról merőlegesek) és a rombuszra (mindkét átló).
  • Végül a homogén négyzet egyszerre téglalap és gyémánt, négy tükörszimmetriatengelye van. Ha "meg van töltve", akkor a szám csökkenthető, amint azt a szomszédos grafika is mutatja.
• A köröknek és a körgyűrűknek végtelen számú szimmetriatengelyük is van, mivel a középponton keresztül minden tengely körül szimmetrikusak.
• Egy másik végtelen számú szimmetriatengelyű ábra az egyenes . Mivel végtelen hosszú, szimmetrikus a rá merőleges tengelyek, valamint a saját tengelye körül.

A függvénygráfok tengelyirányú szimmetriája

Tengelyszimmetrikus függvénygráf

Az iskolai matematikában különösen népszerű feladat a függvény grafikonjának tengelyszimmetriájának bizonyítása. Ez az ellenőrzés különösen egyszerű a (derékszögű) koordinátarendszer y- tengelyének szimmetriája esetén . Egy függvény tengelyirányban szimmetrikus az y tengelyre, ha:

${\ displaystyle f (-x) \, = \, f (x)}$

Ha minden x -re érvényes, akkor van tengelyes szimmetria, vagyis f páros függvény .

Ez a feltétel abból fakad, hogy a függvény értékei az ellentétesen egyenlő argumentumoknak, és meg kell egyezniük. ${\ displaystyle x}$${\ displaystyle -x}$

Általánosabban a következők érvényesek: Az f függvény grafikonja tengelyirányban szimmetrikus az egyenlettel az egyenlettel , és csak akkor, ha az alábbi feltétel minden x értékre igaz: ${\ displaystyle x = a}$

${\ displaystyle f (ax) \, = \, f (a + x)}$

A helyettesítés ezzel egyenértékű feltételt eredményez: ${\ displaystyle x}$${\ displaystyle xa}$

${\ displaystyle f (2a-x) \, = \, f (x)}$

Latin nagybetűs szimmetria

Latin nagybetűs szimmetria

A latin nagybetűk szimmetriái ábrán a 26 betű geometriai szimmetriatulajdonságaik szerint öt csoportra oszlik. Az FHJLPQR betűknek nincs szimmetriájuk. Az NSZ kettős forgásszimmetrikus. Az AMTUVWY szimmetrikus a függőlegeshez, a BCDEK pedig a vízszintes tükörvonalhoz. A négy szimmetriaelemmel rendelkező legmagasabb szimmetria HIOX betűkkel rendelkezik, amelyek kettős forgásszimmetrikusak, és mindegyik vízszintes és függőleges tükörvonallal rendelkezik.

A geometriai szimmetria egyes szavakban is létezik. Az interjekciós OHO például négy szimmetrikus elemet tartalmaz, az OTTO függőleges tükörvonalat, a BOB pedig vízszintes tükörvonalat tartalmaz. Ezek a szavak szintén szó -palindromok . A MENNYEZET és a FŰTÉS tükörszimmetrikus a vízszintes egyenes vonalhoz képest.

Pont szimmetria

Pont szimmetrikus tárgyak a síkban

A pontszimmetria és a központi szimmetria a geometriai objektumok tulajdonsága . A mértani objektum (például négyszög) nevezik (önmagában) pont-szimmetrikus , ha van egy pont reflexió, hogy a képek ezt az objektumot önmagára . A szimmetria középpontjának azt a pontot nevezzük, ahol ez a tükröződés történik .

Példák

• Egy négyzet esetében (önmagában) pontszimmetria akkor és csak akkor létezik , ha paralelogramma . A szimmetria középpontja ebben az esetben az átlóinak metszéspontja. A paralelogramma különleges eseteiként a téglalap , a rombusz és a négyzet is pont-szimmetrikus.
• Minden kör (önmagában) pont-szimmetrikus a középpontjával.
• Két azonos sugarú kör pont-szimmetrikus egymással. A szimmetria középpontja a két kör középpontja közötti összekötő vonal felezőpontja. Pontszimmetria esetén az egymással szimmetrikus vonalak mindig azonos hosszúságúak.

A függvénygráfok pontszimmetriája

Pontszimmetrikus függvénygráf

Az iskolai matematikában különösen gyakori feladat annak bizonyítása, hogy egy adott függvény grafikonja pont-szimmetrikus. Ezt a bizonyítást a következő képlettel lehet megadni:

${\ displaystyle f (a + x) -b = -f (ax) + b}$.

Ha ez az egyenlet minden x esetében teljesül, akkor az ( a, b ) pontra szimmetria van . Az origó (0,0) körüli pontszimmetria különleges esetben ez az egyenlet egyszerűsödik:

${\ displaystyle f (-x) = - f (x)}$.

Ha minden x -re érvényes, akkor a koordináta -eredettel kapcsolatban van pontszimmetria.

Fordítási szimmetria

Fordítási szempontból szimmetrikus rács

Azok az ábrák, amelyeket egy eltolás vagy fordítás önmagává alakít át (ami nem az azonosság), fordítási szimmetriával rendelkeznek . Ezeket időszakosnak is nevezik .

• A transzlációsan szimmetrikus ábráknak szükségszerűen korlátlanoknak kell lenniük. A matematikai alkalmazásokban ez gyakorlatilag soha nem így van, ezért a periodikus halmazok korlátozott részhalmazait ( rács , kristályszerkezet stb.) Periodikusnak nevezzük.
• A periodikus valós függvények, például a szinuszfüggvény grafikonjai egy irányú fordítási szimmetriát mutatnak.

Az alapvektorokat tartalmazó rácsban a fordítási vektor minden pontot elérhet a . A szögek tetszőlegesek. Az alapvektorok szintén átmeneti vektorok, és együtt alkotják az úgynevezett egységcellát .${\ displaystyle {\ vec {\ alpha}}, {\ vec {\ beta}}, {\ vec {\ gamma}}}$${\ displaystyle {\ vec {T}}}$${\ displaystyle u, v, w}$${\ displaystyle {\ vec {\ alpha}}, {\ vec {\ beta}}, {\ vec {\ gamma}}}$

${\ displaystyle {\ vec {T}} = u * {\ vec {\ alpha}} + v * {\ vec {\ beta}} + w * {\ vec {\ gamma}}}$

Skála szimmetria

Néhány matematikai és fizikai környezetben, a változatlanságot egy tárgy alatt a nagyítás vagy kicsinyítés hívják skála a szimmetria vagy skálainvariancia . Ez a jelenség nagyon világossá válik az úgynevezett fraktálokban .

Szimmetria három dimenzióban

Csak a bilateria testének középső sagittalis síkja (mediánsíkja) tükörsík

A természetben

Szimmetria a tüskésbőrűek (pentamerism) _használva a példa a csillag : ötszörös forgástengelye és függőleges tükör sík ( pont-csoport C _5V szerinti Schoenflies )

Az állatfajok túlnyomó többségének testfelépítése , valamint sok növényi szerv felépítése külsőleg szinte tükörszimmetrikus - a biológiában kétoldalúan szimmetrikusnak nevezik - bal és jobb felével. Az egyetlen szimmetriasíkjának (monosymmetry) az anatómiai medián sík , azaz a medián (központi helyen) sagittalis síkban; vagyis a test minden szintje, amely elölről hátulra és felülről lefelé terjed. Az összes állatfaj 95 százaléka, beleértve az embereket is, Bilateria ("kétoldalas állatok"), testük szimmetriájával, amely a nevüket adja (a többi, nagyon eredeti állat (pl. Medúza ) gyakran forgási szimmetriával rendelkezik a hossztengelyhez képest) , így testük közelített A forradalom szilárd ). A bilateria monoszimmetriája miatt a test világos síkjai és irányai határozhatók meg, ami leegyszerűsíti az anatómiai leírást. De a test szimmetriája nem tökéletes, ezért sok egyszerűen előforduló (páratlan) belső szervet (pl. Szív) kizárnak a tükörszimmetriából. Minden szimmetrikusan kialakított testrész, például az emberi szemekben , fülekben , karokban , lábakban , mellekben stb., Mindegyik kis eltéréseket mutat a helyzetben, az alakban és a méretben.

A zoológiában a tüskésbőrűek ötágú sugárirányú szimmetriáját , amely egyedülálló a Bilateria- n belül , pentamerizmusnak nevezik (azaz a tengeri csillagok esetében öt szimmetriasík fut végig a forgás központi tengelyén). A matematikában a tengeri csillag szimmetria tulajdonságait egy forgó csoport írja le. (A tengeri csillagok lárvái kétoldalúan szimmetrikusak, mint a csoport többi állata. A pentamerizmus csak a metamorfózis során alakul ki.)

Szimmetria nélkül, azaz aszimmetrikusan a szövetmentes ( szivacsok és placozák ).

Kétdimenziós szimmetriaelemeknek felel meg

A kétdimenziós tengelyszimmetria megfelel a tükörszimmetriának a háromdimenziós sík vonatkozásában. A pont szimmetria a kétdimenziós megfelel a tengelyirányú szimmetria (forgási szimmetriával körülbelül 180 °). Ezenkívül létezik a térben pont / központi szimmetria , és mint a síkban, a transzlációs szimmetriák .

Forgatási szimmetria / Rotációs szimmetria

Szabályos prizmák forgástengelyekkel és azok számával ( n = 1 azt jelenti: forgásszimmetria nélkül)

A háromdimenziós objektumok szűkebb értelemben forgásszimmetrikusak, ha egy tengely (a szimmetriatengely) körüli bármely szög körüli elforgatás az objektumot önmagára képezi le. Ezt a tengely körüli forgási szimmetriát hengeres szimmetriának is nevezik . Az ilyen tulajdonságú háromdimenziós geometriai tárgyakat forradalmi testeknek is nevezik.

A kétdimenziós analóghoz hasonlóan a forgási vagy forgási szimmetria fogalmát akkor is használják, amikor a testet le lehet képezni önmagára, ha bizonyos szögeket elforgatnak egy tengely körül. A forgásszimmetrikus 3D objektumok példájaként a prizmákat perspektivikusan szemléltetjük a szemközti grafikán , amelyek akkor keletkeznek, amikor a fenti grafika 2D sokszögei Négy szabályos sokszög és két másik geometriai alakzat a forgásszimmetriájuk kulcsfiguráival eltolódnak a térben egy egyenes vonal merőleges az ábra lesz. Ezt az eljárást a sokszög extrudálásának is nevezik . Az eredmény egyenes prizma, speciális poliéder , amelyet ebben az esetben, ha az adott sokszög szabályos sokszög, szabályos prizmának nevezzük.

A 2D objektum szimmetriaközéppontja az extrudálást végző nyílhegy forgástengelyévé válik, amellyel megállapítható, hogy a forgásszöget pozitívnak vagy negatívnak kell -e számítani (lásd a dugóhúzó szabályát ). A szimmetria látható tartozik a gyűrűs csoportok a és alcsoportjainak a megfelelő teljes szimmetrikus csoportjai a prizmák. Meg kell jegyezni, hogy ezek a 3D objektumok további forgási és tükörszimmetriával rendelkeznek. A bemutatott hat szabályos prizmát ábrázolva egy homogén kocka összes forgási szimmetriáját vesszük figyelembe a következő részben . ${\ displaystyle C_ {1}}$${\ displaystyle C_ {6}}$

Egy kocka forgási szimmetriája

A homogén kocka forgásszimmetriájának mind a 13 tengelye

Három négyirányú tengely

Négy háromirányú tengely

Hat 2 számjegyű tengely

Egy homogén kockának összesen 13 forgástengelye van (forgási szimmetriatengelyek), amint az a szomszédos grafikonon látható:

• 3 a felületeket a szemközti oldalak középpontjain keresztül,
• 4 a szemközti sarkokat és
• 6 amelyek a szemközti élek középpontjain haladnak keresztül.

Ha számoljuk a kocka forgásszimmetriájának szimmetria elemeit , akkor ezek a következők: A semleges elem , 3 egyenként 4-szeres, 2-szer 3-szoros és egy-egy kétszeres forgástengely. Mindent összevetve ezek a szimmetria elemei . ${\ displaystyle 1 + 3 \ alkalommal 3 + 4 \ alkalommal 2 + 6 \ alkalommal 1 = 24}$

Ez a 24 elem együtt alkotja a kockaforgató csoportot . Cube és rendszeres oktaéder a kettős platóni testek , és azonos szimmetriák. Ezért a kockaforgató csoporttal és az oktaéder-esztergáló csoporttal együtt foglalkozunk az Octahedron group cikkben . Ha össze a kockát forgatás csoportban a pont reflexió középpontjában a kocka elemeit teljes szimmetria csoportja a kocka eredményét ( lásd alább ). ${\ displaystyle 2 \ cdot 24 = 48}$

Tükör szimmetria

Piazza del Popolo a két (megközelítőleg) tükörszimmetrikus Santa Maria di Monte Santo és Santa Maria dei Miracoli (és az Obelisco Flaminio ) templommal

Négy tükörsík összesen kilencből és egy homogén kocka 13 forgástengelyéből

A tükörszimmetriát két jelentésben használjuk:

• Egy testnek tükörszimmetriája van, ha van sík, és a visszaverődés ezen a síkon a vizsgált test szimmetrikus művelete. A megfigyelt tárgy a tükröződés után egybevág önmagával. A tükör síkja szimmetria is egyszerűen mint a tükör sík . Ebben az értelemben a tükörszimmetria automorfizmus . A matematikában az automorfizmus egy matematikai objektum leképezése önmagára, amelyben az objektum és a leképezett objektum megkülönböztethetetlen.

• Azt mondják, hogy két test tükörszimmetrikus egymással, ha csak egy síkon való tükröződésük különbözik egymástól . Köznyelven az ember tükörfordított másolatról (vagy tükörfordított képről) beszél . A két test térbeli helyzete lényegtelen. Tehát ez lehet szükséges első lépés , és forgatás előtt egy közös tükörsík megtalálható. A két templomok Santa Maria di Monte Santo és Santa Maria dei Miracoli a Piazza del Popolo a Róma vannak (kb) tükör-szimmetrikus és egymással szemben, úgy, hogy a reflexió feltehetően nélkül lehetséges elmozdulását. Az egyházak ekkor szintén tükörszimmetrikusak lennének a fent leírt kifejezés első értelmében. Egy másik klasszikus példája a két tükör-szimmetrikus épület épületek néven King Charles Court és a Queen Anne Bíróság a Royal Naval College in Greenwich, beépített by Christopher Wren .

Az erősen szimmetrikus objektumoknak (mint a szemközti grafikán néhány prizma) nagyszámú tükörsík lehet, amelyek mindegyike egy pontban metszi egymást. Egy gömb végtelen számú tükörsíkkal rendelkezik. A jobb oldali ábrán kilenc tükörsík közül négy és egy homogén kocka 13 forgástengelye látható. A tükörsíkok a 4-szeres forgástengelyben metszik egymást. A bemutatott szimmetria diéderes csoporttípus, és a kockacsoport alcsoportja . A kockacsoport 48 szimmetriaeleme 48 (egyenértékű) alapterületre osztja a kockát . ${\ displaystyle D_ {4}}$

Forgó tükör szimmetria

A forgó tükör szimmetria egy test szimmetriája, amely két részműveletből áll. Az első részművelet egy tengely körüli elforgatás, a forgó tükör tengelye, a második pedig a forgó tengelyre, a forgó tükörsíkra merőleges síkon való tükrözés. Ez a sík átmegy a szimmetria középpontján, a test közepén. Ha a forgó tükörsík nem a test tükörszimmetriasíkja, akkor mindkét részművelet önmagában nem szimmetriaművelet, hanem csak azok kombinációja. A részműveletek sorrendje nem fontos. Először is elvégezhetjük a tükrözést, majd a forgást.

Egy kocka forgó tükörszimmetriája

A homogén kocka kiválasztott forgó tükörtengelyei és forgó tükörsíkai, valamint a forgó tükör hatása

A három 4 számjegyű tengely egyike

A négy 6 számjegyű tengely egyike

A hat 2-szeres tengely egyike (inverzió)

A testek önmagukon történő forgó tükrözése az egyik kevésbé ismert, de talán a legérdekesebb szimmetriaművelet, amely megfelelő grafika segítségével könnyen érthető. A három grafika egy kockát és az egyik forgó tükörtengelyt és a hozzájuk tartozó forgó tükörsíkokat mutatja. A forgó tükörsíkok megkülönböztetéséhez a tükörszimmetriasíkoktól szürke kör alakú korongokként jelennek meg, amelyek vetületesen ellipszisként jelennek meg. A grafikus kockákhoz a félig átlátszó rajzolási módot választottuk. Mivel a forgó tükörtengelyek forgástengelyek, a grafikon sorrendjében lesznek mind a 13 forgási szimmetriatengely felett ... elrendezve.

A három grafika közül az első a három 4-szeres forgó tükörtengely egyikét és a hozzá tartozó forgó tükörsíkot mutatja. A forgó tükrözés hatása megérthető, ha követjük a fehér ponttal jelölt sarok útját. A forgó tükörsík a forgó tükör tengelyén keresztül van irányítva. Ezért azt mondhatjuk, hogy a fehér pont a forgótükör síkja felett van . 90 ° -os elforgatás után (jobbkezes szabály: hüvelykujj a tengely irányába, elforgatás a többi ujj irányába), a pont először a jobb felső sarokba kerül, és tükröződve a jobb alsó sarokba. fekete ponttal van jelölve. A pontot és a képpontot nyíl köti össze. Az új 90 ° -os elforgatás a jobb felső fekete ponthoz vezet, stb.

A kocka egy pontjának útvonala általános helyzetben térbeli, zárt cikk -cakk pálya a forgó tükör síkja körül. Ha az általunk követett pont a forgó tükör síkjában fekszik, akkor annak útvonala négyzet. Ha a forgó tükör tengelyén fekszik, négyszer előre -hátra ugrik a forgó tükör tengelyén, tükrözve a forgó tükörsíkkal. A szimmetria középpontja, a kocka súlypontja mindig önmagára van leképezve. Vegye figyelembe, hogy a forgó tükörsík ebben az esetben a kocka tükörszimmetriasíkja is.

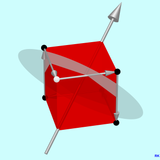
Érdekes a második ábrán látható négy 6-szoros forgó tükörtengely egyik esete. Egyrészt azért érdekes, mert a forgó tükörsík nyilvánvalóan nem a kocka tükörszimmetriasíkja. Másrészt azért, mert a 3-szoros forgástengely hatszoros forgástükör-tengely lesz. Láthatja, hogy 6 számjeggyel rendelkezik, ha követi az útvonalat, amelyet a kocka egy pontja követ, például a grafikonon a fehér ponttal jelölt sarok útvonala. Az első alműveletnél, a forgó tükör tengelye körüli 60 ° -os elforgatással a fehér pont egy olyan pontra lesz leképezve, amely nem sarokpont. A második alművelet, a forgó tükörsíkon való tükrözés az első képponthoz vezet, amely fekete pontként van megjelölve, és amely a forgó tükörsík felett található (fekete pont a jobb felső sarokban). Ismét a pont és a képpont nyíllal van összekötve. Ha most ismét alkalmazza a forgató tükrözést 60 ° -kal az első képpontra, akkor ez a jobb alsó sarokban lévő második fekete képhez vezet, stb. Ha a követendő pont a forgó tükör síkjában fekszik, akkor annak útvonala szabályos hatszög .

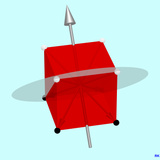
Valószínűleg váratlan a kétszeresen forgó tükrözés hatása, amelyre a harmadik grafika szolgál. Az egyik 2-szeres forgó tükörtengely látható, amelyből a forgótengelyek analógiája alapján hatat várunk. Ha a kétszeres forgó tükrözést a fent vázolt eljárás szerint hajtjuk végre, azt tapasztaljuk, hogy a kocka minden pontja az " antipódjához " van leképezve, vagyis a kocka ellenkező oldalán lévő pontra. A pont és a képpont a szimmetria középpontjával együtt egy egyenes vonalon helyezkedik el, és azonos távolságra vannak a szimmetria középpontjától. Ebben az esetben négy fehér pont van megjelölve a grafikán, és képpontjaik négy feketével. Mind a négy kapcsolatvektor a pont és a képpont között metszi a szimmetria középpontját.

Érdekes megjegyezni azt is, hogy a forgatható tükörképek mind a hat lehetséges 2-szeres forgó tükörtengely körül azonos típusú szimmetriát eredményeznek. Az ilyen típusú szimmetriát, a szimmetria középpontjában lévő pontvisszaverődést a csoportelméletben és a kristálytudományban inverziónak nevezik. Ezért ki lehet hagyni az összes kétszer forgó tükörtengelyt szimmetrikus megfontolásokból, és egyetlen művelettel, az inverzióval helyettesíteni lehet őket.

A forgó tükrözés nem hagy pontot a kockán, azaz nincs sarok, de nincs felület vagy él az eredeti helyükön. A forgó tükrözés egyetlen rögzített pontja a szimmetria középpontja, a kocka középpontja, amelyre már rámutattak.

A három 4-szeres forgó tükörtengely egyike, homogén, szabályos tetraéder forgó tükörsíkjával

Egy homogén, szabályos tetraéder négyszeres forgó tükör szimmetriája is egy homogén kocka, amint azt a grafika egy tengely példájaként mutatja. Amint a grafikából is látható, a kockával ellentétben a forgó tükör síkja nem a tetraéder tükörszimmetria síkja. A grafikán egy burkolókocka drótvázas modellje is rajzolódik.

Különbségek a forgatás tükrözése és a forgatás között

A forgó tükröződések tulajdonságai eltérnek a forgásoktól:

• A test forgástengelyei lehetnek a test forgótükör -tengelyei is, de nem minden forgástengely szükségszerűen forgótükör -tengely. Például a tetraéder esetében a háromszoros forgástengelyei nem forgástengelyek.
• Egy önmagával való forgás szimmetriamûveletének szorzata mindig a csoport új szimmetriaeleme. Egy n-szeres forgástengely esetén a teljesítmény felmegy (n-1) -re. Egy önmagában forgó tükörtengely szimmetrikus működésének szorzata nem a csoport új szimmetriaeleme, hanem (kettős) elforgatás a kettős tükrözés eredményeként.
• A forgástengely és a kiegyenesített forgó tükör tengelyének száma megegyezhet (mindkettő négyjegyű a kocka első grafikonján), vagy eltérő lehet (3 számjegy a forgási szimmetria és 6 számjegy a forgó tükör esetén) szimmetria a második ábrán).
• A kocka minden forgó tükörtengelye két szimmetriaelemmel rendelkezik forgó tükörtengelyenként, függetlenül azok számától. Mivel a kockának három négyjegyű és négy háromjegyű forgó tükörtengelye van, a kockacsoport szűkebb értelemben forgó tükör elemei vannak . Ezen kívül, van egy pont tükrözés minden 2-szeres forgó tükör tengelyek, az inverzió, úgy, hogy összesen 15 forgó tükör elemeket eredményez.${\ displaystyle 2 \ cdot (3 + 4) = 14}$

Amint azt az elején említettük, a pontvisszaverés kétdimenziós kifejezésekkel egyet jelent a rögzített pont körüli 180 ° -os elforgatással, és így nincs külön szimmetriaelem.

Pontszimmetria / inverziós szimmetria

Pontreflexió / inverzió hatása a kocka négy kiválasztott sarkára

Amint azt az előző részben leírtuk, a pontszimmetria vagy az inverziós szimmetria egy test szimmetriája egy ponthoz, a szimmetria középpontjához képest. Mindegyik pont felcseréli pozícióját azzal a ponttal, amely azon az egyenes vonalon van, amely ettől a ponttól a középponton keresztül megy, és a középpont másik oldalán fekszik, azonos távolságra. Ez egy pont tükrözi a test is. A lényeg reflexió nem hagy pont a test az eredeti helyén, egy kivétellel: az egyetlen fix pont a forgatás tükrözi a központja szimmetria a test közepén.

A grafika egy kocka négy kiválasztott sarkának (fehér pontja) inverziós leképezését mutatja (fekete pontok). Ezzel szemben minden fekete pont a fehérre van leképezve. A grafika a fenti harmadik grafika ( kiválasztott forgó tükörtengelyek ... ) ismétlése 2-szeres forgó tükörtengely és forgó tükörsík nélkül.

A homogén platonikus szilárd kocka , oktaéder , dodekaéder és ikozaéder pont-szimmetrikus. Ezzel szemben a legegyszerűbb platóni szilárd anyag, a szabályos tetraéder nem az.

A kocka esetében (beleértve az inverziót is) 15 forgó tükör szimmetria volt. A 9 tükrös szinttel együtt ez 24 szimmetriaelemet eredményez, vagyis pontosan annyi, amennyi a kocka forgó csoport eleme. Ez nem véletlen, mert minden tükör vagy forgó tükör elem a forgás és az inverzió kombinációjaként értelmezhető. Ebben az értelemben az inverz szimmetrikus test inverziója hasonlóan kiemelkedő helyzetben van, mint a szimmetriacsoporton belüli semleges elem.

Gömbszimmetria

A forgásszimmetria bármely tengely körül ugyanazon a ponton keresztül a forgásszimmetria speciális esete, és gömbszimmetriának vagy radiális szimmetriának nevezzük. A csillagok z. B. megközelítőleg gömbszimmetrikus, mivel tulajdonságaik (például a sűrűség) nem mindenhol egyformák, hanem csak a középponttól való távolságtól függenek. Gravitációs mezőik, valamint z. B. a töltött gömb elektromos tere gömbszimmetrikus.

Kombinációk

A szimmetrikus alapműveletek a szimmetriaműveletek kombinálásának lehetőségéből származtathatók:

1. Identitás (nulla művelet, nincs változás)
2. Forgatás ( forgatás )
3. Forgatás - Inverzió ( forgatási tükrözés )
4. Fordítás (elmozdulás)
5. Sikló tükröződés
6. Csavarozás

Lásd még

• Szimmetria (fizika)
• Szimmetria csoport

irodalom

• Hermann Weyl : Szimmetria: Kiegészítve a birtok "Szimmetria és kongruencia" szövegével, valamint Domenico Giulini, Erhard Scholz és Klaus Volkert megjegyzéseivel. Fordító Lulu Hofmann Bechtolsheim . 3. Kiadás. Springer Spektrum, Berlin, Heidelberg 2017, ISBN 978-3-662-52711-5 (VII, 232, korlátozott előnézet a Google könyvkeresőben [hozzáférés: 2019. július 23.]).  Az eredeti 1952 -es újranyomata Hermann Weyl: Symmetry című könyvében . Princeton University Press, Princeton, NJ 2015 (176 pp., Korlátozott előnézet a Google Könyvkeresőben [hozzáférés: 2019. július 23.]). 
• H. Schupp: Elemi geometria . UTB Schöningh 1977, ISBN 3-506-99189-2 , 35., 45. o.
• Will Kleber és mtsai. : Bevezetés a kristálytanba . 19., javított kiadás. Oldenburg Verlag, München 2010, ISBN 978-3-486-59075-3 (470 oldal, korlátozott előnézet a Google könyvkeresőben [hozzáférés: 2019. augusztus 18.]). 
• Werner Hahn: A szimmetria, mint fejlődési elv a természetben és a művészetben . Rupert Riedl előszavával. Koenigstein i. Ts. ( Langewiesche kiadó ) 1989.
• MI Voitsekhovskii: Szimmetria . In: Michiel Hazewinkel (szerk.): Encyclopedia of Mathematics . Springer-Verlag és EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (angol, online ). 
• Arthur Schoenflies: Kristályrendszerek és kristályszerkezet . Teubner, Leipzig 1891 (XII, 638 p., Online források ). 
• David Wade: A szimmetria ereje . Artemis & Winkler Verlag 2011, ISBN 978-3-538-07311-1

web Linkek

Wikiszótár: Szimmetria  - jelentésmagyarázatok, szó eredet, szinonimák, fordítások

Egyéni bizonyíték

1. ↑ A terminológia nem mindig következetes. A rögzített szög körüli forgási szimmetriát forgásszimmetriának is nevezik , hogy megkülönböztessük a forgási szimmetriától , például egy körtől.
2. ↑ Kleber 2010, 52. o
3. ↑ forgási szimmetria. Letöltve: 2019. november 20 . 
4. ↑ ^{a b} Meyer nagy zsebszótára 24 kötetben . BI-Taschenbuchverlag 1992, 21. kötet, 258. o.
5. ↑ Bevezetés az anyagtudományba I. Letöltve: 2020. szeptember 26 . 
6. ↑ tükörsík itt: Richard kormányzás (szerk.): Fizika: 2. kötet / Ma-Z . 2. kiadás. Brockhaus, Lipcse 1989, ISBN 3-325-00192-0 , p.  909 (601-1146, 48 lemez). 
7. ↑ Az autós tükör szimmetria nyilvánvaló kifejezés , amely megkülönbözteti ezt a tükörszimmetriát az első értelemben vett tükörszimmetriától, nem gyakori (nincs találat a Google -on).
8. ↑ Kleber 2010, 60. o.
9. ↑ Ne feledje, hogy az inverzió elnevezést egy kör tükrözésére is használják .
10. ↑ Schoenflies monográfiájának 90. ​​oldalán rámutat arra, hogy ki kell hagyni a kettős tükörszimmetriatengelyeket , amelyeket kettős szimmetriatengelyeknek nevez, és csak inverzióról beszélünk: „Az a művelet, amely a kettős szimmetriatengelyre jellemző. második típus az inverzió A tengely tehát a szimmetria ugyanazt a tulajdonságát képviseli, mint a szimmetria középpontja. De a szimmetria középpontja számára már nincs megkülönböztető irány; a második fajta minden kettős tengelye egyenértékű vele. Emiatt tanácsos teljesen kizárni a második fajta tengelyeit; Ellenkező esetben könnyen felmerülhet az a téves nézet, hogy számukra is a tengely által jelzett irány különleges jelentéssel bír a szimmetria kapcsolódó tulajdonsága szempontjából. "