Tetraéder

Szabályos tetraéder, platonikus szilárd anyag
Oldalsó felületek típusa	egyenlő oldalú háromszögek
Arcok száma	4
A sarkok száma	4
Élek száma	6.
Schläfli ikonra	{3.3}
kettős a	Tetraéder
Test képi háló a két lehetséges háló egyikén
Különböző hálózatok száma	2
A sarkokban lévő élek száma	3
Egy felület sarkainak száma	3
Tetrahedron STL formátumban

A (szintén, különösen Dél-Németországban , a ) tetraéder [ tetraeːdɐ ] (az ókori görög τετρα- tetra „négy”, és ἕδρα HEDRA vagy átruházott „ülés”, „szék”, „vissza”, „oldalával”), még akkor is tetraéder vagy négy lapos , egy test négy háromszög arcok . Ez az egyetlen domború poliéder ( poliéder , poliéder ), amelynek négy oldala van .

A szót azonban ebben az általános értelemben ritkán használják. Általában a tetraéder szabályos tetraéder egyenlő oldalú háromszög , mint oldalsó felületek , amely egy platóni szilárd anyag formájában.

Az általános tetraéder úgynevezett háromoldalú piramis , háromszög alakú piramis , disphenoid vagy háromdimenziós simplex , attól függően, hogy a szimmetria .

Szabályos tetraéder

A szabályos tetraéder ( szabályos tetraéder ) egyike az öt platóni szilárd , pontosabban egy poliéder a

• 4 egybevágó egyenlő oldalú háromszög , mint oldalfelületei
• 6 azonos hosszúságú és
• 4 sarok, ahol három oldalfelület találkozik

A szabályos tetraéder egyenlő oldalú háromoldalú piramis is , amelynek alapja egyenlő oldalú háromszög .

szimmetria

• 

  3 kétszeres szimmetriatengely

• 

  4 háromszoros szimmetriatengely

• 

  A szimmetria 6 szintjének egyike

• 

  A 3 négyszer forgó tükör tengelyének egyike , forgó tükör síkkal

Magas szimmetriája miatt - minden sarka , éle és felülete hasonló egymáshoz - a szabályos tetraéder szabályos poliéder . Megvan

• 4 háromszoros forgástengely ( a szemközti oldalfelületek sarkain és középpontjain keresztül ),
• 3 négyszer forgó tükör tengely és így három kétszeres forgástengely vagy három szimmetria tengely ( az ellentétes élek középpontjain keresztül ) is
• 6 szimmetriasík (mindegyik egy élen át és merőleges a szemközti élre).

Összességében a tetraéder szimmetriacsoportjának - a tetraédercsoportnak - 24 eleme van. Ez a szimmetrikus csoport S ₄ (a -csoportot T _d szerinti Schoenflies vagy 4 3m szerinti Hermann-Mauguin ), és okoz az összes 4! = A sarkok vagy az oldalfelületek 24 permutációja . Ez egy alcsoportja az oktaéder csoport vagy kocka-csoport.

Részletesen a tetraéderes csoportba tartoznak

• 12 forgatás ( egyenletes permutációk ), ti
  • A azonos ábra ,
  • 8 forgatás 120 ° -kal (4 lehetséges forgástengely minden sarkon és a szemközti háromszög felületének középpontján keresztül , 2 lehetőség a forgásirányra) és
  • 3 forgatás 180 ° -kal (forgástengelyek két ellentétes él közepén keresztül)

mint például

• 12 páratlan permutáció . Ezt úgy kapjuk meg, hogy a visszaverődést egy fix szimmetriasíkon hajtjuk végre a 12 egyenletes permutáció után . Ezek közül a 6 tiszta sík tükrözésként is leírható , a másik hat pedig a két ellentétes él középpontján átmenő tengely körüli 90 ° -os elfordulás tükrözésének , valamint az erre a tengelyre merőleges sík tükrözésének , amely a két szemközti él közötti középpont.

A páros permutációk a tetraéderes csoport egy alcsoportját alkotják , az úgynevezett váltakozó csoportot${\ displaystyle A_ {4}}$ (a T vagy 23 pontcsoportot ). Néha a tetraédercsoport kifejezést csak ezekre használják, a reflexiókat leszámítva .

A tetraéder az egyetlen platoni szilárd anyag , amely nem pont-szimmetrikus, és amelyben minden sarok szemben áll egy felülettel .

Egyéb tulajdonságok

Kapcsolat az oktaéderrel, kockával, archimedesi szilárd anyagokkal

A terület középpontjainak összekapcsolásával ismét tetraédert kapunk (lásd az ábrát). Egy Ezért mondja: A tetraéder kettős önmagához , röviden: önduális . A felírt tetraéder oldalhossza az eredeti oldalhossz egyharmada.

Segítségével a két tetraéder szervek lehet kialakítani, amelyek szintén a tetraéder csoport a szimmetria csoport . Tehát kapsz például

• a csonka tetraéder 4 hatszöggel és 4 háromszöggel (lásd Archimedesi szilárd anyag ),
• az oktaéder 4 + 4 = 8 háromszöggel és 6 sarokkal (nagyobb szimmetriával ) két tetraéder metszéspontjaként,
• a csillag-tetraéder (egy oktaéder, amelyhez 8 tetraéder kapcsolódik), mint két tetraéder háromdimenziós egyesülése
• a 4 + 4 = 8 sarkú (és nagyobb szimmetriájú) kocka , mint ennek a csillagtestnek a domború héja .

Lásd még az alábbi példát.

Körülvevő kocka

A tetraéder beírható egy kockába ( hexaéder ) oly módon, hogy sarkai egyidejűleg kocka sarkai , élei pedig a kockafelületek átlói (lásd az ábrát). Ennek a kockának a térfogata a tetraéder térfogatának háromszorosa. A kocka 8 sarka két , négy-négy sarokból álló szétválasztó készletet alkot , amelyek megfelelnek a tetraéder két lehetséges helyzetének.

A Tetrahedron az oktaédert írja le

Ha egy oktaéder körül van egy tetraéder, akkor az oktaéder hat sarka a hat tetraéder élének középpontja, és a nyolc oktaéder arc közül négy a két lehetséges tetraéder egyikének oldalfelületében fekszik .

szög

A kétoldalas szög a szabályos tetraéder két oldalfelülete között  70,53 ° ( ). ${\ displaystyle \ alpha}$${\ displaystyle \ textstyle \ cos \ alpha = {\ frac {1} {3}}}$

Mindegyik él  54,74 ° szöget zár be a felülettel, amelyen áll . ${\ displaystyle \ beta}$${\ displaystyle \ textstyle \ tan \ beta = {\ sqrt {2}}}$

A tetraéder közepe és két sarka közötti összekötő vonalak mindegyike   = 109,47 ° ( ) szöget zár be . ${\ displaystyle \ tau}$${\ displaystyle \ textstyle \ cos \ tau = {- {\ frac {1} {3}}}}$

Ezt tetraéderes szögnek nevezik, és fontos szerepet játszik a kémia területén , például a metán molekula geometriájában .

A megadott szögek méretei trigonometrikus függvények segítségével határozhatók meg (lásd a tompaszög ). Az egyik a tetraéder metszetét nézi (lásd az ábrát) a hat szimmetriasíkjának egyikével .

keresztmetszet

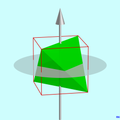
A szabályos tetraéder kettévágható úgy, hogy a vágott felület négyzet alakú legyen . A tetraéder eredő részei egybevágnak egymással.

Ha a szabályos tetraéderen átmenő vágási sík párhuzamos a négy oldalfelület egyikével , akkor a keresztmetszet egyenlő oldalú háromszöget eredményez .

Ha a vágási sík egy szabályos tetraéderen párhuzamosan helyezkedik el két ellentétes éllel, akkor a keresztmetszet egy téglalapot eredményez . Ha a vágási síknak ugyanolyan távolsága van ettől a két éltől, vagyis ha a maradék négy élt pontosan kettéválasztja, akkor a vágási terv négyzet. A négyzet élhossza pontosan a fele a tetraéder egyik szélének.

példa

A tetraéder kockába ágyazása egyszerű módszert kínál a szabályos tetraéder felépítésére. Ha jelöljük a csúcsai a kocka a tövénél , és , valamint a felette fekvő pontok , valamint így formája és és és rendre, a sarkok egy tetraéder. Ha valaki figyelembe veszi a z-t. Például egy háromdimenziós derékszögű koordinátarendszerben azt a kockát kapjuk , amelynek sarkai rendelkeznek a koordinátákkal, és a sarkokat az első tetraéderhez ${\ displaystyle A, B, C}$${\ displaystyle D}$${\ displaystyle E, F, G}$${\ displaystyle H}$${\ displaystyle A, C, F}$${\ displaystyle H}$${\ displaystyle B, D, E}$${\ displaystyle G}$ ${\ displaystyle +1}$${\ displaystyle -1}$

• ${\ displaystyle A (1,1, -1), C (-1, -1, -1), F (-1,1,1)}$és .${\ displaystyle H (1, -1,1)}$

Az élek: és . Az oldalfelületek a háromszögek és . ${\ displaystyle AC, AF, AH, CF, CH}$${\ displaystyle FH}$ ${\ displaystyle ACF, ACH, AFH}$${\ displaystyle CFH}$

A második tetraéder sarka

• ${\ displaystyle B (-1,1, -1), D (1, -1, -1), E (1,1,1)}$és .${\ displaystyle G (-1, -1,1)}$

A háromdimenziós metszéspontja a két tetraéder, hogy a pontok és határozott octahedra . Az unió a csillag tetraéder . A konvex burok tehát a kocka . ${\ displaystyle (1,0,0), (- 1,0,0), (0,1,0) (0, -1,0), (0,0,1)}$${\ displaystyle (0,0, -1)}$

Képletek

Szabályos tetraéder méretei, élhossza a
hangerő	${\ displaystyle V = {\ frac {a ^ {3}} {12}} \ cdot {\ sqrt {2}} \ kb 0 {,} 118 \ cdot a ^ {3}}$	a sarkokban   szilárd szögek nélkül${\ displaystyle \ Omega}$
Felszíni terület	${\ displaystyle A_ {O} = a ^ {2} \ cdot {\ sqrt {3}} \ kb 1 {,} 732 \ cdot a ^ {2}}$
Umkugelradius	${\ displaystyle r_ {u} = 3 \ cdot r_ {i} = {\ frac {a} {4}} \ cdot {\ sqrt {6}} \ kb 0 {,} 612 \ cdot a}$
Élgömb sugara	${\ displaystyle r_ {k} = {\ frac {a} {4}} \ cdot {\ sqrt {2}} \ kb 0 {,} 354 \ cdot a}$
Inc gömb sugara	${\ displaystyle r_ {i} = {\ frac {a} {12}} \ cdot {\ sqrt {6}} \ kb 0 {,} 204 \ cdot a}$
Piramismagasság	${\ displaystyle h_ {p} = r_ {i} + r_ {u} = {\ frac {a} {3}} \ cdot {\ sqrt {6}} \ kb 0 {,} 816 \ cdot a}$
Élettávolság	${\ displaystyle d = 2 \ cdot r_ {k} = {\ frac {a} {2}} \ cdot {\ sqrt {2}} \ kb 0 {,} 707 \ cdot a}$
A térfogat és a gömb térfogat aránya	${\ displaystyle {\ frac {V} {V_ {UK}}} = {\ frac {2 \ cdot {\ sqrt {3}}} {9 \ cdot \ pi}} \ kb 0 {,} 123}$
Az egyenlő oldalú háromszög belső szöge	${\ displaystyle \ alpha = 60 ^ {\ circ}}$
Szög a szomszédos arcok között	${\ displaystyle \ beta = \ arccos \ bal ({\ frac {1} {3}} \ jobb)}$  ${\ displaystyle \ kb. 70 ^ {\ circ} \; 31 ^ {\ prime} \; 44 ^ {\ prime \ prime}}$
Szög az él és az arc között	${\ displaystyle \ gamma = \ arctan \ left ({\ sqrt {2}} \ right)}$  ${\ displaystyle \ kb. 54 ^ {\ circ} \; 44 ^ {\ prime} \; 8 ^ {\ prime \ prime}}$
Tetraéderes szög	${\ displaystyle \ tau = \ arccos \ bal (- {\ frac {1} {3}} \ jobb) \ kb. 109 ^ {\ circ} \; 28 ^ {\ prime} \; 16 ^ {\ prime \ prime }}$
Szögletes szögek a sarkokban	${\ displaystyle \ Omega = \ arccos \ bal ({\ frac {23} {27}} \ jobb) \ kb 0 {,} 5512856 \; \ mathrm {sr}}$
Gömbölyűség	${\ displaystyle \ Psi = {\ sqrt [{3}] {\ frac {\ pi} {6 {\ sqrt {3}}}}} \ kb 0 {,} 671}$

A szabályos tetraéder kiszámítása

hangerő

A piramisokra és így a tetraéderekre is vonatkozik

${\ displaystyle V = {\ frac {1} {3}} \ cdot A_ {G} \ cdot h_ {p},}$

benne van az alapterület ( egyenlő oldalú háromszög )

${\ displaystyle A_ {G} = {\ frac {\ sqrt {3}} {4}} \ cdot a ^ {2}}$

és a piramis magassága

${\ displaystyle h_ {p} = {\ frac {a} {3}} \ cdot {\ sqrt {6}},}$

beillesztett változókkal

${\ displaystyle {\ begin {aligned} V & = {\ frac {1} {3}} \ cdot {\ frac {\ sqrt {3}} {4}} \ cdot a ^ {2} \ cdot {\ frac {a} {3}} \ cdot {\ sqrt {6}} = {\ frac {1} {3}} \ cdot {\ frac {1} {4}} \ cdot {\ frac {1} {3} } \ cdot {\ sqrt {3}} \ cdot {\ sqrt {6}} \ cdot a ^ {3} = {\ frac {1} {12}} \ cdot {\ frac {1} {3}} \ cdot {\ sqrt {3}} \ cdot {\ sqrt {6}} \ cdot a ^ {3} \\ & = {\ frac {a ^ {3}} {12}} \ cdot {\ sqrt {2} } \ kb 0 {,} 118 \ cdot a ^ {3} \ end {igazítva}}}$

A kötet is kiszámítható, mint a különbség egy kockát a élhosszúságú körülírt a szabályos tetraéder , és 4 nem rendszeres tetraéderek, amelyek mindegyike egy közös derékszögű sarok ezzel a kocka. A tetraéder 4 sarka egybeesik a kocka 4 váltakozó sarkával. A 4 nem rendszeres tetraéderek bármelyike 1 oldalfelület közös a szabályos tetraéder, és még 3 derékszögű és egyenlő szárú háromszögek a hossza a átfogója és a hosszát a befogó , mint oldalfelületei. Ez a kathoszthossz ezért felhasználható magasságként a térfogat kiszámításához. ${\ displaystyle {\ tfrac {a} {\ sqrt {2}}}}$ ${\ displaystyle a}$ ${\ displaystyle {\ tfrac {a} {\ sqrt {2}}}}$

Logikusan az eredmény ugyanaz a kötet

${\ displaystyle {\ begin {aligned} V & = balra ({\ frac {a} {\ sqrt {2}}} \ jobbra) ^ {3} -4 \ cdot {\ frac {1} {3}} \ cdot {\ frac {1} {2}} \ cdot \ left ({\ frac {a} {\ sqrt {2}}} \ right) ^ {2} \ cdot {\ frac {a} {\ sqrt { 2}}} = \ left (1-4 \ cdot {\ frac {1} {3}} \ cdot {\ frac {1} {2}} \ right) \ cdot \ left ({\ frac {a} { \ sqrt {2}}} \ right) ^ {3} = {\ frac {1} {3}} \ cdot {\ frac {a ^ {3}} {2 \ cdot {\ sqrt {2}}}} \ \ & = {\ frac {a ^ {3}} {12}} \ cdot {\ sqrt {2}} \ kb 0 {,} 118 \ cdot a ^ {3} \ end {igazítva}}}$

Felszíni terület

A következő a tetraéder felületére vonatkozik (négy egyenlő oldalú háromszög) ${\ displaystyle A_ {O}}$

${\ displaystyle A_ {O} = 4 \ cdot {\ frac {\ sqrt {3}} {4}} \ cdot a ^ {2} = a ^ {2} \ cdot {\ sqrt {3}}.}$

Piramismagasság

A piramis magasságát a következő derékszögű háromszög segítségével lehet meghatározni. ${\ displaystyle h_ {p}}$

Ennek a háromszögnek az oldalhosszai a következők: lásd a képet a képletekben ): az oldalmagasság mint hipotenúz , a piramismagasság, mint egy nagy katéter, és az oldalmagasság egyharmada, mint egy kis katéter. Ezt az értéket az alappont helyzete határozza meg (az alapterület súlypontja). A geometriai súlypont 2: 1 arányban osztja el a háromszög magasságát. ${\ displaystyle h_ {s}}$${\ displaystyle h_ {p}}$${\ textstyle {\ frac {1} {3}} \ cdot h_ {s}}$${\ displaystyle h_ {p}}$

Az alábbiak az egyenlő oldalú háromszög magasságára vonatkoznak${\ displaystyle h_ {s}}$

 ${\ displaystyle h_ {s} = {\ frac {\ sqrt {3}} {2}} \ cdot a}$

és a Pitagorasz-tétel szerint

${\ displaystyle {\ begin {aligned} \; h_ {p} ^ {2} & = h_ {s} ^ {2} - \ left ({\ frac {1} {3}} \ cdot h_ {s} \ jobbra) ^ {2} = h_ {s} ^ {2} - {\ frac {1} {9}} \ cdot h_ {s} ^ {2} = {\ frac {8} {9}} \ cdot h_ {s} ^ {2} \; \ Rightarrow \\ & = {\ frac {8} {9}} \ cdot {\ frac {3} {4}} \ cdot a ^ {2} = {\ frac {2 } {3}} \ cdot a ^ {2} \ Rightarrow \\ h_ {p} & = {\ sqrt {{\ frac {2} {3}} \ cdot a ^ {2}}} = {\ sqrt { \ frac {2} {3}}} \ cdot a = {\ frac {a} {3}} \ cdot {\ sqrt {6}}. \; \ end {igazítva}}}$

Szög a szomszédos arcok között

Ennek a szögnek, amelyet jelölünk , a tetraéder egyik szélén van a csúcsa. A következő derékszögű háromszög segítségével határozható meg. ${\ displaystyle \ beta}$

Ennek a háromszögnek az oldalhosszai a következők: lásd a képet a képletekben ): az oldalmagasság mint hipotenusz , a piramismagasság, mint egy nagy katetus, és az oldalmagasság (lásd a magasságokat ) egy része, mint egy kis katétus. ${\ displaystyle h_ {s}}$${\ displaystyle h_ {p}}$${\ textstyle {\ frac {1} {3}} \ cdot h_ {s}}$

A Pitagorasz-tétel szerint a következők érvényesek

${\ displaystyle {\ begin {aligned} \; \ cos \ beta & = {\ frac {\ frac {h_ {s}} {3}} {h_ {s}}} = {\ frac {{\ frac {1 } {3}} \ left ({\ frac {\ sqrt {3}} {2}} \ right) \ cdot a} {{\ frac {\ sqrt {3}} {2}} \ cdot a}} = {\ frac {1} {3}} \ Rightarrow \\\ beta & = \ arccos \ left ({\ frac {1} {3}} \ right) \ kb 70 ^ {\ circ} \; 31 ^ {\ prime} \; 44 ^ {\ prime \ prime} \; \ end {igazítva}}}$

Szög az él és az arc között

Ennek a szögnek, amelyet jelölünk , a tetraéder egyik sarkában van a csúcsa. A szöget a következő derékszögű háromszög segítségével lehet meghatározni. ${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$

Ennek a háromszögnek az oldalhosszúsága (lásd a képleteken látható képet ): a piramis széle, mint a hipotenusz , a piramis magassága, mint a nagy katéter, és az oldalmagasság egy része (lásd a magasságokat ), mint a kis katetosz. ${\ displaystyle a}$${\ displaystyle h_ {p}}$${\ textstyle {\ frac {2} {3}} \ cdot h_ {s}}$

A következő a szögre vonatkozik${\ displaystyle \ gamma}$

${\ displaystyle {\ begin {aligned} \; \ tan \ gamma & = {\ frac {h_ {p}} {{\ frac {2} {3}} \ cdot h_ {s}}} = {\ frac { {\ frac {a} {3}} \ cdot {\ sqrt {6}}} {{\ frac {2} {3}} \ cdot {\ frac {\ sqrt {3}} {2}} \ cdot a }} = {\ frac {{\ frac {1} {3}} \ cdot {\ sqrt {6}}} {{\ frac {1} {3}} \ cdot {\ sqrt {3}}}} = {\ sqrt {2}} \ Rightarrow \\\; \\\ gamma & = \ arctan \ left ({\ sqrt {2}} \ right) \ kb 54 ^ {\ circ} \; 44 ^ {\ prime} \; 8 ^ {\ prime \ prime} \; \ end {igazítva}}}$

Tetraéderes szög

Ennek a szögnek a jelölése csúcsa a tetraéder közepén van. A szög a következő derékszögű háromszög segítségével határozható meg. ${\ displaystyle \ tau}$${\ displaystyle \ tau}$

Ennek a háromszögnek az oldalhosszai a következők: lásd a képet a képletekben : Umkugelradius mint hipotenúz , az élhossz fele nagy katetusként, a fele pedig az éltávolságtól, mint egy kis katéter . ${\ displaystyle r_ {u}}$${\ textstyle {\ frac {1} {2}} \ cdot a}$${\ textstyle {\ frac {1} {2}} \ cdot d}$

A következő a szögre vonatkozik${\ displaystyle \ tau}$

${\ displaystyle {\ begin {aligned} \; \ cos {\ frac {\ tau} {2}} & = {\ frac {\ frac {d} {2}} {r_ {u}}} = {\ frac {\ frac {{\ frac {a} {2}} \ cdot {\ sqrt {2}}} {2}} {{\ frac {a} {4}} \ cdot {\ sqrt {6}}}} = {\ frac {{\ frac {a} {4}} \ cdot {\ sqrt {2}}} {{\ frac {a} {4}} \ cdot {\ sqrt {6}}}} = {\ frac {1} {\ sqrt {3}}} \ Rightarrow \\\ cos \ tau & = \ cos \ left (\ arccos \ left ({\ frac {1} {\ sqrt {3}}} \ right) \ cdot 2 \ right) = - {\ frac {1} {3}} \ Rightarrow \\\ tau & = \ arccos \ left (- {\ frac {1} {3}} \ right) \ kb. 109 ^ {\ circ} \; 28 ^ {\ prime} \; 16 ^ {\ prime \ prime} \ kb 1 {,} 910633236249 \, \ mathrm {rad} \ end {igazítva}}}$

Szögletes szögek a sarkokban

A következő képlet, amelyet a Platonic Solids ír le, a szilárd szög megoldását mutatja${\ displaystyle \ Omega}$

${\ displaystyle \ Omega = 2 \ pi -2n \ cdot \ arcsin \ left (\ cos \ left ({\ frac {\ pi} {n}} \ right) \ cdot {\ sqrt {\ tan ^ {2} \ bal ({\ frac {\ pi} {n}} \ jobb) - \ tan ^ {2} \ bal ({\ frac {\ alpha} {2}} \ jobb)}} \ jobb)}$

Ha az élek / oldalak száma egy sarokban van, és az egyenlő oldalú háromszög belső szöge az alábbiakra vonatkozik ${\ displaystyle {n = 3}}$${\ displaystyle {a = 60 ^ {\ circ}}}$

${\ displaystyle {\ begin {aligned} {\ mathsf {(1)}} \; \ Omega & = 2 \ pi -2 \ cdot 3 \ cdot \ arcsin \ left (\ cos \ left ({\ frac {\ pi } {3}} \ right) \ cdot {\ sqrt {\ tan ^ {2} \ left ({\ frac {\ pi} {3}} \ right) - \ tan ^ {2} \ left ({\ frac {60 ^ {\ circ}} {2}} \ right)}} \ right) \ Rightarrow \\ & = 2 \ pi -6 \ cdot \ arcsin \ left ({\ sqrt {\ frac {2} {3} }} \ jobbra) \ kb 0 {,} 551285598 \; \ mathrm {sr} \\\ end {igazítva}}}$

mert ez ${\ displaystyle \ cos (\ arcsin x) = {\ sqrt {1-x ^ {2}}}}$

${\ displaystyle {\ begin {aligned} {\ mathsf {(2)}} \; \ cos (\ arcsin x) & = {\ sqrt {1- \ left ({\ sqrt {\ frac {2} {3} }} \ jobbra) ^ {2}}} = {\ frac {1} {\ sqrt {3}}} \ Rightarrow \\\ end {aligned}}}$

használt in és képződött ${\ displaystyle {\ mathsf {(2)}}}$${\ displaystyle {\ mathsf {(1)}}}$

${\ displaystyle {\ begin {aligned} {\ mathsf {(3)}} \; \ Omega & = 2 \ pi -6 \ cdot \ arccos \ left ({\ frac {1} {\ sqrt {3}}} \ right) \ kb 0 {,} 551285598 \; \ mathrm {sr} \; \ end {igazítva}}}$

egyszerűsítés

${\ displaystyle {\ begin {aligned} {\ mathsf {(4)}} \; \ cos \ Omega & = \ cos \ left (2 \ pi -6 \ cdot \ arccos \ left ({\ frac {1} { \ sqrt {3}}} \ right) \ right) = {\ frac {23} {27}} \ Rightarrow \\\ end {aligned}}}$

${\ displaystyle {\ begin {aligned} {\ mathsf {(5)}} \; \ Omega & = \ arccos \ left ({\ frac {23} {27}} \ right) \ kb 0 {,} 551285598 \ ; \ mathrm {sr}. \; \ end {igazítva}}}$

A szabályos tetraéder hálói

A tetraédernek két hálója van (lásd a képeket). Ez azt jelenti, hogy kétféle módon lehet egy üreges tetraédert kibontani, ha 3 szélét nyitjuk és kiterítjük a síkba . A másik 3 él összeköti a hálózat 4 egyenlő oldalú háromszögét . Ahhoz, hogy a szín egy tetraéder, így nem szomszédos arcok az azonos színű, akkor kell 4 színben.

• 
• 

Grafikonok, kettős grafikonok, ciklusok, színek

A tetraéder van egy irányítatlan síkbeli gráf 4 csomópont , 6 élek és 4 régiók hozzárendelve. Ez a teljes K ₄ grafikon . Ez 3 szabályos , azaz 3 él kezdődik minden csomópontból, így a fok minden csomópontnál 3. Síkgrafikonok esetében a csomópontok pontos geometriai elrendezése jelentéktelen. Fontos azonban, hogy az éleknek ne kelljen keresztezniük egymást. Ennek a tetraédergráfnak a csomópontjai megfelelnek a tetraéder sarkainak.

A tetraéder gráf csomópontjai 4 színnel színezhetők, így a szomszédos csomópontok mindig másképp színezhetők, mivel minden csomópont szomszédos. Ez azt jelenti, hogy ennek a grafikonnak a kromatikus száma 4 (lásd a csomópont színezését ). Ezenkívül az élek 3 színnel színezhetők úgy, hogy a szomszédos élek mindig eltérő színűek legyenek (lásd illusztrációk). Ez 2 színnel nem lehetséges, ezért az élszínezés kromatikus indexe 3 (a jobb oldali kép szemlélteti ezeket a színezéseket).

A tetraéderes gráf önduális .

A területekhez vagy területekhez szükséges színek számának meghatározásához hasznos a kettős gráf , amely ebben az esetben maga egy tetraéder gráf , 4 csomópontgal , 6 éllel és 4 területtel. Ennek a grafikonnak a csomópontjai egy az egyhez (bijektív) vannak hozzárendelve az eredeti tetraéder grafikon területeihez és fordítva (lásd a bijektív függvényt és a fenti ábrát). Mint már említettük, a kettős tetraéder gráf csomópontjai nyilvánvalóan csak 4 színnel színezhetők úgy, hogy a szomszédos csomópontok mindig másképp legyenek színezve. Ebből közvetve következtethetünk: Mivel a kromatikus szám egyenlő 4-tel, 4 színre van szükség a tetraéder ilyen felületi színezéséhez vagy a tetraéder területeinek színezéséhez.

Az egyes hálózatok (lásd fent) 3 vágott éle a sarkokkal ( csomópontokkal ) együtt alkot egy átfogó fát a tetraédergrafikonból. Minden hálózat pontosan megfelel egy átfogó fának és fordítva, így egy-egy ( bijektív ) hozzárendelés van a hálózatok és az átfogó fák között. Ha a külső terület nélküli tetraéderhálózatot grafikonnak tekintjük , kapunk egy kettős gráfot , amelynek fája 4 csomópontú, 3 élű és a maximális csomópontfoka 3. . A 2 gráfelméleti konstelláció (lásd a grafikonok izomorfizmusát ) egyszerre fordul elő.

A tetraéderes grafikonon 6 Hamilton kör van , Euler körök viszont nincsenek .

Szobatöltések szabályos tetraéderekkel

A háromdimenziós euklideszi tér teljesen kitölthető ugyanolyan élhosszúságú platóni vagy archimedesi szilárd anyagokkal . Az ilyen háromdimenziós fedés van úgynevezett szobában tölteléket . A következő űrkitöltések tetraédereket tartalmaznak:

• 

  Szoba töltő és oktaéder és tetraéder

• 

  A szoba megtöltése csonka tetraéderrel és tetraéderrel

• 

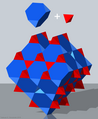
  A szoba kitöltése rombikus cuboctahedronnal , kocka és tetraéderrel

Alkalmazások

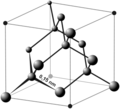
Bár a tetraéder nem a helyiség parkettájának köve, a köbös kristályrendszerben fordul elő (lásd fent).

A kémiában , a tetraéder játszik jelentős szerepet a térbeli elrendezése atomok a vegyületek . Az egyszerű molekuláris alakok a VSEPR modellel megjósolhatók. A négy hidrogénatomok a metánmolekulával vannak elrendezve tetraéderesen körül szénatom , mivel ez az, hogy a kötés szög a legnagyobb. A gyémántrács szénatomjai szintén tetraéderes módon vannak elrendezve, mindegyik atomot négy másik atom veszi körül. A szénatom majd miután az orbitális modell sp ³ - hibridizáció .

A tetraéder eredeti alakja miatt a Tetra Pak névadója is volt .

Alexander Graham Bell többsejtű dobozos sárkányokkal (sárkányokkal) kísérletezett, amelyek egyes sejtjei tetraéder alakúak. Ezeket a többnyire impozáns sárkányokat "Bell Tetrahedron" -nak hívják. Általában 4 vagy 10 vagy 20 egyedi sejtet állítanak össze, így összetett képződik, amelynek ezután ismét tetraéder alakja van. Más kompozit formák is lehetségesek.

Számos toll és papír szerepjátékban a tetraédereket négyoldalú játékkockákként használják (D4).

A további technikai alkalmazások azon a struktúrán alapulnak, amely a tetraéder közepétől a szoba négy sarkáig mutató vonalakból származik:

• Tetrapodák , amelyeket hullámtörőként használnak a partokon
• úgynevezett szarkalábak , egy védekező fegyver, amelyet a rendőrség és a katonaság használ az autók ellen abroncsaik felrobbantása érdekében.

• 

  Beton tetrapod a Helgolandon

• 

  A gyémánt rács egységcellája

• 

  Varjúlábnyira a Stratégiai Szolgáltatások Irodája

• 

  Space keretrendszerhez készült tetraéderek

Általános tetraéder

Az általános értelemben vett tetraéder , azaz négy oldalú test mindig háromoldalú piramis , vagyis háromszög az alapja és három háromszöge az oldala, ezért négy sarka és hat éle is van . Mivel a lehető legkevesebb sarka és oldala van egy testnek az űrben, technikai értelemben háromdimenziós szimplexnek vagy 3- szimplexnek hívják . A kétdimenziós egyszerűségek a háromszögek.

• Mindegyik 3- egyszerûnek van egy umkugelje és egy incugelje .
• A súlypont a metszéspontja az összekötő vonalak között, a sarkok és a súlypontok a szemközti háromszögek és elválasztja őket arányban 3: 1 ( Commandino-tétel ).
• Minden 3 szimplex négy sarkának domború héja .
• A Szilassi- poliéder mellett ez az egyetlen ismert poliéder , amelyben minden oldal szomszédos egymással.

Egy tetraéderben egy ponttal is lehet, és a három vektort leírjuk a szomszédos pontokra. Ha ezeket a vektorokat a -val jelöljük , akkor a tetraéder térfogatát , azaz a köpött termék mennyiségét kell kiszámítani . ${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle {\ vec {a}}, {\ vec {b}}, {\ vec {c}}}$${\ displaystyle \ textstyle V = {\ frac {1} {6}} \ cdot \ left | \ det \ left [{\ begin {smallmatrix} {\ vec {a}} \\ {\ vec {b}} \ \ {\ vec {c}} \ end {smallmatrix}} \ right] \ right | = {\ frac {1} {6}} \ cdot \ left | ({\ vec {a}} \ szor {\ vec { b}}) \ cdot {\ vec {c}} \ right |}$${\ displaystyle {\ frac {1} {6}}}$

Az egyenletesen kifelé vagy befelé mutató normál egységvektorok összege , amelyet megszorzunk annak a felületnek a tartalmával, amelyen áll, nulla vektor , mert

${\ displaystyle {\ vec {a}} \ times {\ vec {b}} + {\ vec {b}} \ times {\ vec {c}} + {\ vec {c}} \ times {\ vec { a}} + ({\ vec {c}} - {\ vec {a}}) \ szor ({\ vec {b}} - {\ vec {a}}) = {\ vec {0}}}$

Bármely tetraéder kiszámítása

A tetraéder 6 éllel rendelkezik. A háromszöget három oldalhossz megadásával lehet meghatározni. Minden további él bizonyos határok között szabadon választható. Ha 6 független információ áll rendelkezésre az élek vagy szögek méretéről , akkor ezek alapján kiszámíthatja a hiányzó éleket vagy szögeket.

hangerő

Az általános tetraéder térfogati képletét Leonhard Euler adta meg . Ezzel a képlettel kiszámítható az általános tetraéder térfogata a tetraéder 6 élhosszának segítségével. Így a kötet képlet általános tetraéder azonos feladatot tetraéderes alapon a háromszögek a képlet Heron .

Ha a szélén hossza háromszög alapja a tetraéder, és a hossza a szemközti éleinek a térben , akkor a következő érvényes, hogy a térfogata a tetraéder: ${\ displaystyle a, b, c}$ ${\ displaystyle a ', b', c '}$ ${\ displaystyle V}$

${\ displaystyle V = {\ tfrac {1} {12}} \ cdot {\ sqrt {a ^ {2} \ cdot a '^ {2} \ cdot f_ {a} + b ^ {2} \ cdot b' ^ {2} \ cdot f_ {b} + c ^ {2} \ cdot c '^ {2} \ cdot f_ {c} - \ delta}}}$

Val vel

${\ displaystyle f_ {a} = b ^ {2} + b '^ {2} + c ^ {2} + c' ^ {2} -a ^ {2} -a '^ {2}}$

${\ displaystyle f_ {b} = a ^ {2} + a '^ {2} + c ^ {2} + c' ^ {2} -b ^ {2} -b '^ {2}}$

${\ displaystyle f_ {c} = a ^ {2} + a '^ {2} + b ^ {2} + b' ^ {2} -c ^ {2} -c '^ {2}}$

${\ displaystyle \ delta = a ^ {2} \ cdot b ^ {2} \ cdot c ^ {2} + a ^ {2} \ cdot b '^ {2} \ cdot c' ^ {2} + a ' ^ {2} \ cdot b ^ {2} \ cdot c '^ {2} + a' ^ {2} \ cdot b '^ {2} \ cdot c ^ {2}}$

A szimmetrikus mátrixok determinánsain alapuló következő egyenletek szintén felhasználhatók a térfogat kiszámításához :

${\ displaystyle {\ begin {aligned} 288 \ cdot V ^ {2} & = \ det {\ begin {pmatrix} 0 & c ^ {2} & b ^ {2} & a '^ {2} & 1 \ \ c ^ {2} & 0 & a ^ {2} & b '^ {2} & 1 \\ b ^ {2} & a ^ {2} & 0 & c' ^ {2} & 1 \\ a '^ {2} & b' ^ {2} & c '^ {2} & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \\\ end {pmatrix}} \\ & = \ det {\ kezdődik {pmatrix} 2 \ cdot c ^ {2} & c ^ {2} + b ^ {2} -a ^ {2} & c ^ {2} + a '^ {2} -b' ^ {2} \\ c ^ {2} + b ^ {2} -a ^ {2} & 2 \ cdot b ^ {2} & b ^ {2} + a '^ {2} -c' ^ {2} \\ c ^ {2} + a '^ {2} -b' ^ {2} & b ^ {2} + a '^ {2} - c' ^ {2} & 2 \ cdot a '^ {2} \ \\ end {pmatrix}} \\\ end {igazítva}}}$

Az első meghatározó az úgynevezett Cayley - Menger meghatározó és használják kiszámításához a terület bármely háromszög (lásd Heron-tétel ), a kötet minden tetraéder és általában a kötet minden simplex a dimenziós térben . ${\ displaystyle n}$

Felszíni terület

A terület egy háromszög a megadott oldalsó hosszúságú lehet kiszámítani egyenként. A 4 háromszög területének összege adja a tetraéder területét. A Heron tétel szerint például a háromszög alakú alap oldalhosszúságú területére : ${\ displaystyle a, b, c}$

${\ displaystyle A = {\ frac {1} {4}} \ cdot {\ sqrt {(a + b + c) \ cdot (-a + b + c) \ cdot (a-b + c) \ cdot (a + időszámításunk előtt)}}}$

Magasság

Mivel minden tetraéder egy piramis , a következő egyenlet érvényes a térfogat , a terület a bázis és a megfelelő magasság : ${\ displaystyle V}$ ${\ displaystyle A}$ ${\ displaystyle h}$

${\ displaystyle V = {\ frac {A \ cdot h} {3}}}$

${\ displaystyle h = {\ frac {3 \ cdot V} {A}}}$

A térfogat és a terület kiszámítható a fenti képletek segítségével, majd felhasználható a magasság meghatározásához. A másik három magasság ennek megfelelően kiszámítható a magasságra merőleges háromszög területével . ${\ displaystyle V}$ ${\ displaystyle A}$

A háromszögek belső szögei

A belső szöge a háromszögek segítségével határozzuk meg a törvény koszinuszok . Például az alapnak az oldallal szemben lévő belső szöge érvényes ${\ displaystyle \ alpha}$${\ displaystyle a}$

${\ displaystyle \ alpha = \ arccos \ left ({\ frac {b ^ {2} + c ^ {2} -a ^ {2}} {2 \ cdot b \ cdot c}} \ jobb)}$

Szög a szomszédos arcok között

A szélén lévő kétágú szög${\ displaystyle a}$

${\ displaystyle \ beta = \ arcsin \ balra ({\ frac {3 \ szor egy V-szeresére} {2 \ -szer A_-re {1} \ -szer A_-re {2}}} \ jobbra)}$

Itt látható a térfogata a tetraéder és és a terület a háromszög mellett a szélét . ${\ displaystyle V}$${\ displaystyle A_ {1}}$${\ displaystyle A_ {2}}$

Vannak a belső szögek , , egy sarkon , ahol a tetraéder, és , , a diéderes szögek közötti szomszédos felületek ebben a sarokban, akkor szerint a koszinusz törvény gömb alakú háromszögek a egyenlet${\ displaystyle \ alpha _ {i, j}}$${\ displaystyle \ alpha _ {i, k}}$${\ displaystyle \ alpha _ {i, l}}$${\ displaystyle \ beta _ {i, j}}$${\ displaystyle \ beta _ {i, k}}$${\ displaystyle \ beta _ {i, l}}$

${\ displaystyle \ cos (\ alpha _ {i, j}) = \ cos (\ alpha _ {i, k}) \ cdot \ cos (\ alpha _ {i, l}) + \ sin (\ alpha _ { i, k}) \ cdot \ sin (\ alpha _ {i, l}) \ cdot \ cos (\ beta _ {i, j})}$

Ebből következik

${\ displaystyle \ beta _ {i, j} = \ arccos \ left ({\ frac {\ cos (\ alpha _ {i, j}) - \ cos (\ alpha _ {i, k}) \ cdot \ cos (\ alpha _ {i, l})} {\ sin (\ alpha _ {i, k}) \ cdot \ sin (\ alpha _ {i, l})}} \ jobbra}}$

A dihedrális szögeket és szintén megkapjuk .${\ displaystyle \ beta _ {i, k}}$${\ displaystyle \ beta _ {i, l}}$

Szögletes szögek a sarkokban

A belső szöge a három szomszédos háromszög használjuk kiszámításához szilárd szögek a sarkokban a tetraéder : ${\ displaystyle \ theta _ {a}, \ theta _ {b}, \ theta _ {c}}$

${\ displaystyle \ Omega = 4 \ cdot \ arctan \ left ({\ sqrt {\ tan \ left ({\ frac {\ theta _ {s}} {2}} \ right) \ cdot \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {a}} {2}} \ right) \ cdot \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {b}} {2 }} \ jobbra) \ cdot \ tan \ balra ({\ frac {\ theta _ {s} - \ theta _ {c}} {2}} \ jobbra)}} \ jobbra)}$

Val vel

${\ displaystyle \ theta _ {s} = {\ frac {\ theta _ {a} + \ theta _ {b} + \ theta _ {c}} {2}}}$

Számítás a koordinátákból

Vannak a koordinátákat , , , a sarkok ismert a tetraéder, az oldalsó hosszak a euklideszi távolságok${\ displaystyle (x_ {1}, y_ {1}, z_ {1})}$${\ displaystyle (x_ {2}, y_ {2}, z_ {2})}$${\ displaystyle (x_ {3}, y_ {3}, z_ {3})}$${\ displaystyle (x_ {4}, y_ {4}, z_ {4})}$

${\ displaystyle s_ {i, j} = {\ sqrt {(x_ {i} -x_ {j}) ^ {2} + (y_ {i} -y_ {j}) ^ {2} + (z_ {i } -z_ {j}) ^ {2}}}}$

sarkok mindenki számára . ${\ displaystyle i, j \ \ {1,2,3,4 \}}$${\ displaystyle i \ neq j}$

Ha és két irányvektor , hogy indítsa el az azonos sarkában a tetraéder, akkor megkapjuk a belső szöge ebben sarok ${\ displaystyle {\ vec {a}} = {\ begin {pmatrix} x_ {j} -x_ {i} \\ y_ {j} -y_ {i} \\ z_ {j} -z_ {i} \ end {pmatrix}}}$${\ displaystyle {\ vec {b}} = {\ begin {pmatrix} x_ {k} -x_ {i} \\ y_ {k} -y_ {i} \\ z_ {k} -z_ {i} \ end {pmatrix}}}$ ${\ displaystyle \ alpha}$

${\ displaystyle \ alpha = \ arccos \ left ({\ frac {{\ vec {a}} \ cdot {\ vec {b}}} {| {\ vec {a}} | \ cdot | {\ vec {b }} |}} \ jobbra}}$

ahol a skalár terméket és , és a hossza a vektorok és a . ${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}}}$${\ displaystyle | {\ vec {a}} |}$${\ displaystyle | {\ vec {b}} |}$ ${\ displaystyle {\ vec {a}}}$${\ displaystyle {\ vec {b}}}$

A térfogat meghatározható a meghatározó segítségével

${\ displaystyle V = {\ frac {1} {6}} \ cdot \ det {\ begin {pmatrix} x_ {1} & y_ {1} & z_ {1} & 1 \\ x_ {2} & y_ { 2} & z_ {2} & 1 \\ x_ {3} & y_ {3} & z_ {3} és 1 \\ x_ {4} & y_ {4} & z_ {4} és 1 \\\ end { pmatrix}}}$

kell kiszámítani.

A definíció mint ponthalmaz

A szabályos tetraéder lehet meghatározni , mint egy sor a pontokat a háromdimenziós euklideszi térben a szélén gömb sugara . Formálisan ez az összeg leírható ${\ displaystyle r_ {k} = {\ tfrac {a} {4}} \ cdot {\ sqrt {2}}}$

${\ displaystyle \ left \ {(x_ {1}, x_ {2}, x_ {3}) \ in \ mathbb {R} ^ {3} \ x x {1} + x_ {2} + x_ {3} \ leq r_ {k} \ \ land \ x_ {1} -x_ {2} -x_ {3} \ leq r_ {k} \ \ land \ -x_ {1} + x_ {2} -x_ {3} \ leq r_ {k} \ \ land \ -x_ {1} -x_ {2} + x_ {3} \ leq r_ {k} \ right \}}$

A belsejében a tetraéder kell lennie a 4 egyenlőtlenségek minden esetben az kell cserélni, és a felület legyen 1, 2 vagy 3 egyenlőtlenségek által kell cserélni, úgy, hogy a rendszer az egyenletek és egyenlőtlenségek létre. 1 egyenlet alapján a mennyiség meghatározza a tetraéder oldalfelületét, azaz egyenlő oldalú háromszöget , 2 egyenlettel élt és 3 egyenlettel a sarkát. ${\ displaystyle \ leq}$${\ displaystyle <}$${\ displaystyle \ leq}$${\ displaystyle =}$

E meghatározás szerint a szabályos tetraéder középpontja a koordináták eredete, 4 sarka pedig egy körülhatárolt kocka 4 váltakozó sarka, amelynek oldalhossza van , amelynek élei és oldalfelületei párhuzamosan futnak a derékszögű tengely 3 tengelyével. koordináta-rendszer . ${\ displaystyle 2 \ cdot r_ {k}}$

Általánosabban: egy szabályos tetraéder, amelynek bármilyen helyzete van a háromdimenziós euklideszi térben , vektorok segítségével definiálható. Van a helyvektora a központ és , , ortogonális irányvektorok összekötő közepén a tetraéder 3 középpontjának 3 élek, így egy ortogonális rendszerben, a háromdimenziós vektortér űrlapot, majd a levelek mennyisége a pontokat a tetraéder a vektorok mennyiségeként definiálva${\ displaystyle {\ vec {m}}}$${\ displaystyle {\ vec {u}}}$${\ displaystyle {\ vec {v}}}$${\ displaystyle {\ vec {w}}}$ ${\ displaystyle \ mathbb {R} ^ {3}}$

${\ displaystyle \ left \ {{\ vec {m}} + t_ {1} \ cdot {\ vec {u}} + t_ {2} \ cdot {\ vec {v}} + t_ {3} \ cdot { \ vec {w}} \ in \ mathbb {R} ^ {3} \ t_ közepén {1} + t_ {2} + t_ {3} \ leq r_ {k} \ \ land \ t_ {1} -t_ { 2} -t_ {3} \ leq r_ {k} \ \ land \ -t_ {1} + t_ {2} -t_ {3} \ leq r_ {k} \ \ land \ -t_ {1} -t_ { 2} + t_ {3} \ leq r_ {k} \ right \}}$

általánosítás

A tetraéder általánosításait bármely dimenzióban -dimenziós szimplexeknek nevezzük . A dimenziós simplex van sarkok és határolja a simplexes a dimenzió (például oldalait ). A nulla dimenziós szimplex egy pont , az egydimenziós szimplex egy szakasz , a kétdimenziós szimplex egy háromszög , a háromdimenziós pedig egy tetraéder. A tetraéder négydimenziós megfelelőjének, a pentachoronnak 5 sarka , 10 éle, 10 háromszöge van, és 5 háromdimenziós tetraéderje van. ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n + 1}$${\ displaystyle n + 1}$${\ displaystyle n-1}$

Az koordinátáit rendszeres - dimenziós szimplex lehet meghatározni, mint egy set in dimenziós euklideszi térben : ${\ displaystyle n}$ ${\ displaystyle n}$

${\ displaystyle \ left \ {x \ in \ mathbb {R} ^ {n} \ {\ Bigg |} \ \ sum _ {i = 1} ^ {n} x_ {i} = x_ {1} + x_ { 2} + \ ldots + x_ {n + 1} \ leq 1 \ \ land \ \ forall i: \ - (n + 1 + {\ sqrt {n + 1}}) \ cdot x_ {i} + \ sum _ {i = 1} ^ {n} x_ {i} \ leq 1 \ \ right \}}$

vagy egy set in dimenziós euklideszi térben${\ displaystyle n + 1}$

${\ displaystyle \ left \ {x \ in \ mathbb {R} ^ {n + 1} \ {\ Bigg |} \ \ sum _ {i = 1} ^ {n + 1} x_ {i} = x_ {1 } + x_ {2} + \ ldots + x_ {n + 1} = 1 \ \ land \ \ mind i: \ x_ {i} \ geq 0 \ \ right \}}$

Például egy eredmény itt egyenlő oldalú háromszög , ami a pontokat , , a háromdimenziós térben kifeszített.${\ displaystyle n = 2}$ ${\ displaystyle (1,0,0)}$${\ displaystyle (0,1,0)}$${\ displaystyle (0,0,1)}$

Sierpinski tetraéder

A Sierpinski-tetraéder a Sierpinski-háromszög háromdimenziós általánosítása . A kiinduló ábra egy tetraéder. Mindegyik iterációs lépésben egy középpontjából kivágunk egy élhossz felével rendelkező oktaédert . Marad 4 tetraéder, amelyek mindegyikéből kivágnak egy oktaédert stb.

Az iterációs lépés után nyilvánvalóan azonos részhosszúságú részleges tetraéderek jelentek meg. A számos vágott ki octahedra a különböző oldalak hosszát is . ${\ displaystyle k}$${\ displaystyle 4 ^ {k}}$${\ displaystyle {\ frac {4 ^ {k} -1} {3}}}$

Ennek a szerkezetnek a dimenziója , bár ez egy ábra a háromdimenziós térben. Egyre több iterációs lépésnél az ábra térfogata nulla, de a felület területe állandó marad, mert az egybevágó részleges tetraéderek oldalfelületeinek száma minden egyes iterációs lépésnél megnégyszereződik, míg ezen oldalfelületek oldalhossza , amelyek mindegyike egybevágó háromszög, a felére csökken. ${\ displaystyle D = {\ frac {\ log (4)} {\ log (2)}} = 2}$

Lásd még

• Reuleaux-tetraéder
• Tetraéder számok
• Diederwinkel
• poliéder
• Platonikus szilárd anyag
• Tetrapod (kő)

irodalom

• Heinz Schumann: Elemi tetraéderes geometria . Franzbecker, Hildesheim 2011, ISBN 978-3-88120-521-4

web Linkek

• Euklidész: Stoicheia. XIII.13. Könyv. Egy gömb szeletelője ...
• Tetrahedron . Matek bütykölés

Egyéni bizonyíték

1. ↑ Kurt Peter Müller: Térgeometria: Téri jelenségek - Konstruktúra - Számítás . 2., átdolgozott és kibővített kiadás. Vieweg + Teubner, 2004, ISBN 978-3-519-12397-2 , 81. o.
2. ↑ Jürgen Köller: Tetrahedron. A tetraédertől a többi testig. math-tinkering, megtekintve: 2020. szeptember 5 . 
3. ↑ Eric Weisstein, Frank Jackson: Rendszeres tetraéder. Umkugelradius, (5) képlet. In: MathWorld Wolfram. Egy Wolfram webes erőforrás, hozzáférés 2020. június 19 . 
4. ↑ Eric Weisstein, Frank Jackson: Rendszeres tetraéder. Élgömb sugara, (10) képlet. In: MathWorld Wolfram. Egy Wolfram webes erőforrás, hozzáférés 2020. június 19 . 
5. ↑ Eric Weisstein, Frank Jackson: Rendszeres tetraéder. Gömbön belüli sugár, (4) képlet. In: MathWorld Wolfram. Egy Wolfram webes erőforrás, hozzáférés 2020. június 19 . 
6. ↑ Harish Chandra Rajpoot: A platonikus szilárd testek (szabályos poliéderek) által lefedett szilárd szögek a csúcsaikban. SlideShare, 2015. március, hozzáférés: 2020. június 16 . 
7. ↑ A kifejezés alternatív kifejezése . ${\ displaystyle \ cos \ Omega}$WolramAlpha, hozzáférés: 2020. június 16 . 
8. ↑ Eric Weisstein, Frank Jackson: Rendszeres tetraéder. 2 hálózat, az (1) képlet felett. In: Wolfram MathWorld. A Wolfram Research, Inc. hozzáférése: 2020. június 19 . 
9. ^ Wolfram MathWorld: Tetraéder grafikon
10. ^ Maximilian Miller: Sztereometria. 1957, 41. o
11. ↑ Az E 231 értekezés címe németül nagyjából a következő: Néhány jellemző tulajdonság bemutatása, amelyekkel a sík felületekkel körülvett testek fel vannak szerelve . Ebben az értekezésben Euler az első bizonyítékot adja a sokszög képletről , amelyet már egy korábbi értekezésében adott ( E 230 , Elementa doctrinae solidorum alatt nyomtatva , Novi commentarii academiae scientiarum Petropolitanae 4, 109–140. Oldal; vö. Bevezetés a Commentationes-be geometricae ) említett, de még nem bizonyított.
12. ^ Andreas Speiser és mtsai: Leonhardi Euleri Opera omnia. Nagyszerű sorozat. Opera mathematica. XXVI. Kötet: Commentationes geometricae. I. kötet, 1953., 106–107
13. ^ IN Bronstein, KA Semendjajev et al.: Taschenbuch der Mathematik. 2008, 157. o
14. ^ Hajós György: Bevezetés a geometriába. 1970, 383. o
15. ↑ Alexander Ostermann, Gerhard Wanner: Geometry by History. 2012, 297. o
16. ↑ Veremcsere : A tetraéderfelületek közötti kétdimenziós szögek a hegyen lévő háromszögek szögeiből
17. ^ G. Richardson: A tetraéder trigonometria . In: A Matematikai Közlöny . 2, 32. szám, 1902. március 1., 149-158. doi : 10.2307 / 3603090 .
18. ^ Wolfram MathWorld: Tetrahedron
19. ^ Wolfram MathWorld: Rendszeres tetraéder
20. ^ Martin Henk, Jürgen Richter-Gebert, Günter M. Ziegler, Berlini Technische Universität: A konvex politopok alapvető tulajdonságai
21. ^ Wolfram MathWorld: Tetrix
22. ↑ Gayla Chandler, Hideki Tsuiki: Fotók: Sierpinski Tetrahedron és kiegészítése