Integrált számítás

A felül eltérés fogkő, integrálszámítás a legfontosabb ága a matematikai fegyelem elemzés . A terület- és térfogatszámítás problémájából adódott. Az integrál egy általános kifejezés a határozatlan és a határozott integrálra. Az integrálok számítását integrációnak nevezzük .

A határozott integrál egy függvény egy számot hozzá. Ha egy valós függvény határozott integrálja egy változóban van kialakítva , akkor az eredmény a kétdimenziós koordinátarendszerben úgy értelmezhető, mint a terület azon területe, amely a függvény grafikonja, az -axis és a -tengely. Itt a tengely alatti területek negatívnak számítanak . Az egyik a tájolt felületről (a felszíni egyensúlyról is ) beszél . Ezt a konvenciót úgy választjuk meg, hogy a határozott integrál egy lineáris leképezés , amely az integrál fogalmának központi tulajdonsága mind elméleti megfontolások, mind konkrét számítások szempontjából. Ez biztosítja azt is, hogy a differenciál- és integrálszámítás úgynevezett főtétele érvényesüljön. ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle x}$

A függvény határozatlan integrálja ezt sok tulajdonsághoz rendeli, a primitív függvények elemeit hívják. Ezeket az jellemzi, hogy első deriváltjaik megfelelnek az integrált függvénynek. A differenciál- és integrálszámítás fő tétele információt nyújt arról, hogyan lehet bizonyos integrálokat kiszámítani az antiderivatívumokból.

A differenciálással ellentétben nincs egyszerű algoritmus, amely minden esetre kiterjed az elemi függvények integrálására is . Az integráció gyakorlott találgatást, speciális átalakítások alkalmazását ( helyettesítéssel történő integráció , részleges integráció ), integrált táblázatban való keresést vagy speciális számítógépes szoftver használatát igényli . Az integráció gyakran csak megközelítőleg történik úgynevezett numerikus kvadratúra segítségével .

A technológiában a hozzávetőleges területmeghatározáshoz ún . Az így meghatározott terület számértéke leolvasható egy számlálón, amely vernierrel van ellátva az olvasási pontosság növelése érdekében . A vegyészek analitikai mérleget vagy mikromérleget használtak bármely terület integráljának meghatározására: a területet óvatosan kivágták és lemérték, akárcsak ugyanannak a papírnak a darabját, pontosan 10 cm × 10 cm méretű ; a hármas szabály vezetett eredményre.

sztori

A területszámításokat az ókortól kezdve tanulmányozták. A Kr. E. 5. században Knidos -i Eudoxus az Antiphon ötlete alapján kifejlesztette a kimerülési módszert , amely abból állt , hogy zárt vagy átfedő sokszögek segítségével megbecsülték a felületek arányát . Ezzel a módszerrel meg tudta határozni néhány egyszerű test területét és térfogatát. Archimedes (ie 287–212) javította ezt a megközelítést, és így sikerült pontosan meghatároznia a parabolikus ív és a secant által határolt terület területét anélkül, hogy igénybe vette volna a határ fogalmát , amely akkor még nem volt elérhető; ez az eredmény könnyen átalakítható ma ismert másodfokú függvény integráljává. Azt is megbecsülte a kerület és az átmérő arányát ,, és között . ${\ displaystyle \ pi}$${\ displaystyle \ texttyle {3 {\ frac {10} {71}}}}$${\ displaystyle \ texttyle {3 {\ frac {10} {70}}}}$

Ezt a módszert a középkorban is alkalmazták. A 17. században Bonaventure Francesco Cavalieri megalkotta a Cavalieri elvét , amely szerint két test térfogata azonos, ha minden párhuzamos síkmetszet azonos területtel rendelkezik. Johannes Kepler Astronomia Nova (1609) című munkájában olyan módszerekkel számította ki a Mars pályáját, amelyeket ma numerikus integrációnak neveznek. 1612 -től a boroshordók térfogatát próbálta kiszámítani. 1615 -ben kiadta a Stereometria Doliorum Vinariorum -ot (" Borhordók sztereometriája "), amelyet később Kepler hordószabályának is neveztek .

A 17. század végén Isaac Newtonnak és Gottfried Wilhelm Leibniznek egymástól függetlenül sikerült számításokat fejlesztenie a differenciálszámításhoz, és így felfedeznie az elemzés alaptételét (a felfedezés történetét és az elsőbbségi vitát lásd. cikk Végtelen kicsi számítás ; az integráljelet és annak történetét lásd az integráljelben ). Munkája lehetővé tette a pusztán geometriai elképzelések absztrakcióját, ezért az elemzés kezdetének tekintik. Őket a könyv révén ismerte meg legjobban Guillaume François Antoine nemes , de L'Hospital márki , aki magánórákat vett Johann I Bernoullitól, és publikálta az elemzéssel kapcsolatos kutatásait. Az integrál kifejezés Johann Bernoulli -ra nyúlik vissza.

A 19. században minden elemzés szilárdabb alapokra helyeződött. 1823 - ban Augustin-Louis Cauchy először kifejlesztett egy integrált kifejezést, amely megfelel a mai szigorúság követelményeinek . A Riemann -integrál és a Lebesgue -integrál feltételei később merültek fel . Végül a mértékelmélet fejlődése következett a 20. század elején.

Integrált a kompakt intervallumokhoz

A „kompakt” itt korlátozottat és zártat jelent, ezért csak az űrlap időközönként történő funkcióit vesszük figyelembe. Nyílt vagy korlátlan időközök nem megengedettek. ${\ displaystyle [a, b]}$

motiváció

Az összetett területek integrálokra redukálása

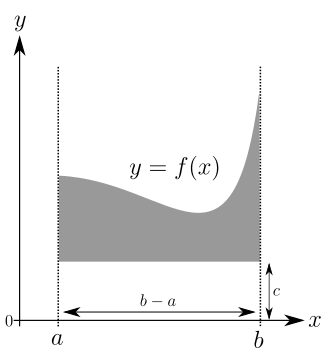
Az integrálszámítás egyik célja a sík görbe vonalú területeinek területének kiszámítása. A gyakorlatban előforduló esetek többségében az ilyen területeket két folyamatos függvény írja le kompakt időközönként , amelyek grafikonjai korlátozzák a területet (bal oldali kép). ${\ displaystyle f, g}$${\ displaystyle [a, b]}$

: :

A bal oldali kép szürke területe megegyezik a két jobb oldali kép szürke területeinek különbségével. Tehát elegendő az egyszerűbb esetre korlátozódni, ha egy terület határol:

• függvény grafikonja
• két függőleges egyenes és${\ displaystyle x = a}$${\ displaystyle x = b}$
• valamint a tengely.${\ displaystyle x}$

Alapvető fontossága miatt ez a fajta terület különleges nevet kap:

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$,

olvasni, mint integrál legfeljebb körülbelül${\ displaystyle a}$${\ displaystyle b}$ (vagy a ) az , . Ma a faktort általában tiszta jelölési komponensként használják, és az -axis differenciáját jelenti . Ahelyett, hogy egy másik változót választanánk azon kívül és például , ami nem változtatja meg az integrál értékét. ${\ displaystyle f}$${\ displaystyle x}$${\ displaystyle \ mathrm {d} x}$ ${\ displaystyle \ mathrm {d} x}$${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle t}$

Integrált negatív függvények

Ha egy függvény grafikonját egy kicsit eltolja az -axis irányába , akkor egy négyszög kerül hozzáadásra a vizsgált területhez: ${\ displaystyle y}$${\ displaystyle c}$

:

Az integrál ennek a téglalapnak a szélesség és magasság területe szerint változik a képletekben ${\ displaystyle ba}$${\ displaystyle c}$

${\ displaystyle \ int _ {a} ^ {b} (f (x) + c) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (x) \, \ mathrm {d } x + (ba) \ cdot c.}$

Ha egy folytonos függvényt nézünk, amelynek értékei negatívak, mindig találhatunk a -t, így az intervallum értékei mind pozitívak ( nagyobbnak kell lenniük, mint az in minimumának abszolút értéke ). A fentiek figyelembevételével az ember megkapja ${\ displaystyle c \ in \ mathbb {R}}$${\ displaystyle f (x) + c}$${\ displaystyle c}$${\ displaystyle f}$${\ displaystyle [a, b]}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = \ int _ {a} ^ {b} (f (x) + c) \, \ mathrm {d } x- (ba) \ cdot c,}$

vagyis integrálja a különbség a középen lévő fehér terület és a környező téglalap területei között. Ez a különbség azonban negatív, vagyis ha a fenti képlet bármely funkcióhoz igaz, a tengely alatti területeket negatívnak kell számítani. Az egyik tehát orientált vagy irányított területről beszél . ${\ displaystyle f}$${\ displaystyle x}$

Ha a vizsgálandó intervallumban egy vagy több nulla található, akkor az integrál már nem a területet jelzi, hanem az -axis feletti részterületek (pozitív) területeinek összegét és az alatta lévő részterületek (negatív) területeit az -axis. Ha ilyen intervallumban szüksége van az -axis és a függvény grafikonja közötti területre , akkor az integrált nullákra kell osztani. ${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$

Cavalieri elve és az integrál additivitása

Axiomatikus megközelítés

Nem könnyű matematikailag pontosan felfogni a terület fogalmát. Az idők folyamán különféle koncepciókat dolgoztak ki erre. A legtöbb alkalmazás esetében azonban részleteik irrelevánsak, mivel többek között megegyeznek a folyamatos függvények osztályában. Az alábbiakban felsoroljuk az integrál néhány tulajdonságát, amelyeket a fentiek motiváltak, és amelyek minden integrálra vonatkoznak, függetlenül a pontos felépítéstől. Ezenkívül egyértelműen meghatározzák a folyamatos függvények integrálját.

Legyen valós számok , és legyen egy vektortér funkciók , hogy magában foglalja a folytonos függvények . A függvényeket integrálhatónak nevezik. Akkor integrál a térkép ${\ displaystyle a <b}$ ${\ displaystyle {\ mathcal {F}}}$${\ displaystyle [a, b] \ to \ mathbb {R}}$${\ displaystyle {\ mathcal {F}}}$

${\ displaystyle {\ mathcal {F}} \ to \ mathbb {R},}$

írott

${\ displaystyle f \ mapsto \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x,}$

a következő jellemzőkkel:

• Linearitás: Függvényekre és alkalmazható ${\ displaystyle f, g \ in {\ mathcal {F}}}$${\ displaystyle \ lambda \ in \ mathbb {R}}$
  • ${\ displaystyle \ int _ {a} ^ {b} (f (x) + g (x)) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x + \ int _ {a} ^ {b} g (x) \, \ mathrm {d} x}$,
  • ${\ displaystyle \ int _ {a} ^ {b} lambda f (x) \, \ mathrm {d} x = \ lambda \ cdot \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$.
• Monotónia: Mindenkinek szól , így van ${\ displaystyle f (x) \ geq 0}$${\ displaystyle x \ itt: [a, b]}$

  ${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x \ geq 0.}$

• Az intervallum jellemző funkciójának integrálja : intervallum és van${\ displaystyle I \ subseteq [a, b]}$

${\ displaystyle \ chi _ {I} (x) = {\ begin {case} 1 \, & \ mathrm {if} \ x \ in I \, \\ 0 \, & \ mathrm {if} \ x \ notin Én \, \ vége {esetek}}}$

így is van

${\ displaystyle \ int _ {a} ^ {b} \ chi _ {I} (x) \, \ mathrm {d} x}$

egyenlő az intervallum hosszával .${\ displaystyle I}$

Megnevezések

• A valós számok és az úgynevezett integrációs korlátok. Felírhatók az integráljel fölé és alá, vagy az integráljel mellé:${\ displaystyle a}$${\ displaystyle b}$

${\ displaystyle {\ texttyle \ int \ limits _ {a} ^ {b}} f (x) \, {\ rm {d}} x}$     vagy     ${\ displaystyle \ int \ nolimits _ {a} ^ {b} f (x) \, {\ rm {d}} x}$

• Az integrálandó függvényt integrand -nak nevezzük .${\ displaystyle f}$
• A változót integrációs változónak nevezik . Ha az integráció változó, akkor az egyik is beszél az integráció kb . Az integrációs változó helyettesíthető${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle x}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$

ugyanúgy megteheti

${\ displaystyle \ int _ {a} ^ {b} f (t) \, \ mathrm {d} t}$ vagy ${\ displaystyle \ int _ {a} ^ {b} f (\ xi) \, \ mathrm {d} \ xi}$

írni. A fenti példában a betűk használata vagy nemkívánatos félreértésekhez vezet, mivel ezek már az integrációs korlátok azonosítói. Ezért győződjön meg arról, hogy az integrációs változóhoz használt karakterhez már nem tartozik más jelentés.${\ displaystyle a}$${\ displaystyle b}$

• A „ ” komponenst differenciálnak nevezik, de ebben az összefüggésben többnyire csak szimbolikus jelentése van. Ezért itt nem tesznek kísérletet annak meghatározására. Az integrációs változó leolvasható a differenciálból.${\ displaystyle \ mathrm {d} x}$

A jelölés eredete

Az integrálok szimbolikus helyesírása a differenciál- és integrálszámítás első leírójához, Gottfried Wilhelm Leibnizhez nyúlik vissza . Az integrál jel ∫ származik a levél hosszú s (k) a latin summa . A multiplikatív jelölés azt jelzi, hogy az integrál - a Riemann -integrált követve - hogyan áll a magasság és a végtelen kicsi szélesség csíkjaiból . ${\ displaystyle f (x) \; \ mathrm {d} x}$${\ displaystyle f (x)}$${\ displaystyle \ mathrm {d} x}$

Alternatív helyesírás a fizikában

Az elméleti fizikában pragmatikai okokból gyakran használnak egy kissé eltérő jelölést az integráloknál (különösen több integrál esetében). Ott tartják

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$

gyakran

${\ displaystyle \ int _ {a} ^ {b} \ mathrm {d} xf (x)}$

néha mindkét írásmódot különböző helyeken használják.

A második példa hátránya, hogy az integrálandó funkciót nem zárójelek és zárójelek veszik figyelembe . Ezenkívül félreértések is előfordulhatnak, például a Lebesgue integrál esetében . Az alternatív jelölésnek azonban néhány előnye is van: ${\ displaystyle f (x)}$${\ displaystyle \ texttyle \ int _ {a} ^ {b}}$${\ displaystyle \ mathrm {d} x}$

• A kifejezés hangsúlyozza, hogy az integrál egy lineáris operátor, amely minden tőle jobbra hat.${\ displaystyle \ texttyle \ int _ {a} ^ {b} \ mathrm {d} x}$
• A fizikában gyakran megjelennek integrálok, amelyekben az integrálandó funkció több sor hosszú, vagy több ismeretlenbe van integrálva . Akkor már az integrál elején tudja, hogy mely változók vannak integrálva és melyek a határértékek. Ezenkívül könnyebb a változók korlátozásokhoz rendelése.${\ displaystyle x_ {1}, x_ {2}, \ dotsc, x_ {n}}$${\ displaystyle \ texttyle \ int _ {a} ^ {b} \ mathrm {d} xf (x)}$
• Hangsúlyozzák a termékek kommutativitását a Riemann -közelítésben előforduló összehívásokban .${\ displaystyle \ Delta x_ {n} \ cdot f (x_ {n})}$

Példa:

${\ displaystyle \ int _ {a_ {1}} ^ {a_ {2}} \ mathrm {d} t \ int _ {b_ {1}} ^ {b_ {2}} \ mathrm {d} x_ {1} \ int _ {c_ {1}} ^ {c_ {2}} \ mathrm {d} x_ {2} \ int _ {d_ {1}} ^ {d_ {2}} \ mathrm {d} x_ {3} \, f (x_ {1}, x_ {2}, x_ {3}, t)}$

ahelyett

${\ displaystyle \ int _ {a_ {1}} ^ {a_ {2}} \ int _ {b_ {1}} ^ {b_ {2}} \ int _ {c_ {1}} ^ {c_ {2} } \ int _ {d_ {1}} ^ {d_ {2}} f (x_ {1}, x_ {2}, x_ {3}, t) \, \ mathrm {d} x_ {3} \ mathrm { d} x_ {2} \ mathrm {d} x_ {1} \ mathrm {d} t}$

Az axiómák egyszerű következményei

• Van mindenkinek , így${\ displaystyle f (x) \ leq g (x)}$${\ displaystyle a \ leq x \ leq b}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x \ leq \ int _ {a} ^ {b} g (x) \, \ mathrm {d} x. }$

• Ha az egyik jelentése a supremum norma az on , akkor a következő érvényes${\ displaystyle \ | f \ | _ {\ infty}}$${\ displaystyle f}$${\ displaystyle [a, b]}$

${\ displaystyle \ left | \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x \ right | \ leq (ba) \ cdot \ | f \ | _ {\ infty}.}$

• Van minden rögzített számú , majd alkalmazni${\ displaystyle | f (x) -g (x) | <\ varepsilon}$${\ displaystyle a \ leq x \ leq b}$${\ displaystyle \ varepsilon> 0}$

${\ displaystyle \ left | \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x- \ int _ {a} ^ {b} g (x) \, \ mathrm {d} x \ jobb | \ leq (ba) \ cdot \ varepsilon.}$

Ebből következik: Ha az integrálható függvények sorozata egyenletesen konvergál egy (integrálható) függvényhez , akkor ${\ displaystyle (f_ {n}) _ {n \ in \ mathbb {N}}}$${\ displaystyle f}$

${\ displaystyle \ lim _ {n \ to \ infty} \ int _ {a} ^ {b} f_ {n} (x) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x.}$

Más szóval: az integrál folyamatos funkció a szupremum normához.

• Integrálok lépés funkciók: Ha egy lépcsős függvény , ami van, egy diszjunkt egyesítését a időközönként a hossz , úgyhogy a jelentése konstans érték , akkor érvényes${\ displaystyle f}$${\ displaystyle [a, b]}$${\ displaystyle I_ {k}}$${\ displaystyle L_ {k}}$${\ displaystyle f}$${\ displaystyle I_ {k}}$${\ displaystyle c_ {k}}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = \ sum _ {k = 1} ^ {n} L_ {k} \ cdot c_ {k},}$

így egyértelműen megegyezik a függvénygráf és a tengely közötti téglalapok orientált területeinek összegével .${\ displaystyle f}$${\ displaystyle x}$

Antiderivatívumok és a differenciál- és integrálszámítás fő tétele

Az integráció a differenciálódás kétértelmű megfordítása. Ahhoz, hogy ezt a pontosabb, a koncepció egy antiderivált van szükség: Ha egy függvény, akkor a függvény hívódik egy primitív az , ha a származékot a van egyenlő : ${\ displaystyle f}$${\ displaystyle F}$${\ displaystyle f}$${\ displaystyle F}$${\ displaystyle f}$

${\ displaystyle F '= f}$

Ez az inverzió kétértelmű, mert a különböző függvényeknek (pl. Polinomfüggvények, amelyek csak az Y-tengely metszéspontjában különböznek) egy és ugyanaz a deriváltjuk lehet, ami azt jelenti, hogy egy függvénynek nemcsak egy, hanem végtelen számú antiderivatívja van.

A differenciál- és integrálszámítás fő tétele megállapítja az antiderivatívumok és az integrálok közötti kapcsolatot. Azt mondja: Ha egy folyamatos függvény egy intervallumon, és egy antiderivatív , akkor van ${\ displaystyle f}$${\ displaystyle [a, b]}$${\ displaystyle F}$${\ displaystyle f}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = F (b) -F (a).}$

A jobb oldalt gyakran rövidítik:

${\ displaystyle [F (x)] _ {a} ^ {b} = [F (x)] _ {x = a} ^ {x = b} = F (x) {\ Big |} _ {a} ^ {b} = F (x) {\ Nagy |} _ {x = a} ^ {x = b}}$ vagy hasonló

írott.

Ez az összefüggés a fő módszer az integrálok explicit értékeléséhez. A nehézség általában az antiderivatívum megtalálása.

A puszta létezés elméletileg biztosított: az integrálfüggvény

${\ displaystyle x \ mapsto \ int _ {a} ^ {x} f (t) \, \ mathrm {d} t}$

mindegyikre antiderivatív . ${\ displaystyle a}$${\ displaystyle f}$

Az antiderivatívumok tulajdonságai

Egy konstanst hozzáadhat az antiderivativhez, és újra antiderivative -t kaphat: Ha az antiderivative egy függvényhez tartozik, és állandó, akkor ${\ displaystyle F}$${\ displaystyle f}$${\ displaystyle c \ in \ mathbb {R}}$

${\ displaystyle (F + c) '= F \! \,' + 0 = F '= f.}$

Ugyanazon függvény két, intervallumon meghatározott antiderivatívja konstansban különbözik egymástól: Ha és ugyanazon függvény antiderivatívumai , akkor ${\ displaystyle F}$${\ displaystyle G}$${\ displaystyle f}$

${\ displaystyle (FG) \! \, '= F'-G' = ff = 0,}$

tehát a különbség állandó. Ha a tartomány a meghatározás nem egy intervallum, akkor a különbség a két antiderivatives csak lokálisan konstans . ${\ displaystyle FG}$${\ displaystyle f}$

Határozatlan integrál

Egy primitív is nevezik határozatlan integrál az - de néha azt is jelenti, a készlet minden antiderivatives. Ha antiderivatívum, akkor gyakran pontatlanul írják ${\ displaystyle f (x)}$${\ displaystyle F (x)}$

${\ displaystyle \ int f (x) \, \ mathrm {d} x = F (x) + C,}$

jelezni, hogy minden antiderivatívum alakja állandó . Az állandót az integráció állandójának nevezzük .${\ displaystyle f}$${\ displaystyle F (x) + C}$${\ displaystyle C}$${\ displaystyle C}$

Vegye figyelembe, hogy a jelölés

${\ displaystyle \ int f (x) \, \ mathrm {d} x}$

azonban gyakran használják képletekben is annak jelzésére, hogy az egyenletek érvényesek tetszőleges, következetesen választott határokra; például vele van

${\ displaystyle \ int cf (x) \, \ mathrm {d} x = c \ int f (x) \, \ mathrm {d} x}$

azt jelentette, hogy

${\ displaystyle \ int _ {a} ^ {b} cf (x) \, \ mathrm {d} x = c \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x}$

bármelyikre érvényes . ${\ displaystyle a, b}$

Az antiderivatívumok meghatározása

Lásd a cikket: Derivált és antiderivatívumok vagy határozatlan integrálok táblázata a matematikai képletgyűjteményben .

A derivált függvénnyel ellentétben az antiderivatívusz kifejezett számítása nagyon nehéz vagy lehetetlen sok funkció esetében. Ez az oka annak, hogy az integrálokat gyakran táblázatokban keresik fel (pl . Integrált táblázat ). Az antiderivatívum kézi számításához gyakran hasznos az alábbi szabványos technikák ügyes használata.

Részleges integráció

A részleges integráció a differenciálszámítás szorzata . Ez:

${\ displaystyle \ int _ {a} ^ {b} f '(x) \ cdot g (x) \, \ mathrm {d} x = [f (x) \ cdot g (x)] _ {a} ^ {b} - \ int _ {a} ^ {b} f (x) \ cdot g '(x) \, \ mathrm {d} x}$

Ez a szabály akkor hasznos, ha a függvény könnyebben integrálható, mint a függvény . Itt azonban nem a termékeket, hanem magukat a tényezőket kell értékelni. ${\ displaystyle f (x) \ cdot g '(x)}$${\ displaystyle f '(x) \ cdot g (x)}$

Példa:

${\ displaystyle \ int _ {a} ^ {b} x \ ln (x) \, \ mathrm {d} x}$

Ha beállítottad

${\ displaystyle f '(x) = x \,}$ és ${\ displaystyle g (x) = \ ln (x) \,}$

így is van

${\ displaystyle f (x) = {\ frac {x ^ {2}} {2}}}$ és ${\ displaystyle g '(x) = {\ frac {1} {x}}}$

és kapsz

${\ displaystyle {\ begin {aligned} \ int _ {a} ^ {b} x \ ln (x) \, \ mathrm {d} x & = {\ frac {b ^ {2}} {2}} \ ln (b) - {\ frac {a ^ {2}} {2}} \ ln (a) - \ int _ {a} ^ {b} {\ frac {x ^ {2}} {2}} \ cdot {\ frac {1} {x}} \, \ mathrm {d} x \\ & = {\ frac {b ^ {2}} {2}} \ bal (\ ln (b) - {\ frac { 1} {2}} \ jobb) - {\ frac {a ^ {2}} {2}} \ bal (\ ln (a) - {\ frac {1} {2}} \ jobb). \ Vége { igazítva}}}$

Integráció helyettesítéssel

A helyettesítési szabály fontos eszköz néhány nehéz integrál kiszámításához, mivel lehetővé teszi a funkció bizonyos módosításainak integrálását, miközben megváltoztatja az integrációs korlátokat. Ez a párja a differenciálszámítás láncszabályának .

Hagyja , hogy legyen és legyen antiderivatívum , akkor antiderivative , mert ez érvényes ${\ displaystyle \ varphi (x) = f (g (x)) \ cdot g '(x)}$${\ displaystyle g '\ neq 0}$${\ displaystyle F}$${\ displaystyle f}$${\ displaystyle \ Phi (x) = F (g (x))}$${\ displaystyle \ varphi}$

${\ displaystyle {\ frac {\ varphi (x)} {g '(x)}} = f (g (x))}$

és a helyettesítéssel

${\ displaystyle z = g (x), \ quad \ mathrm {d} z = g '(x) \ mathrm {d} x}$

a végén

${\ displaystyle {\ begin {aligned} \ int _ {a} ^ {b} f (g (x)) g '(x) \ mathrm {d} x & = \ int _ {g (a)} ^ { g (b)} f (z) \ mathrm {d} z \\ & = F (g (b)) - F (g (a)) \\ & = \ Phi (b) - \ Phi (a). \ end {igazítva}}}$

Átalakítás részleges frakcióbontással

Tört-racionális függvények esetén a polinomiális osztás vagy a részleges törtbontás gyakran a függvény átalakításához vezet , ami lehetővé teszi az egyik integrációs szabály alkalmazását.

Különleges eljárások

Gyakran lehetséges az antiderivatívum meghatározása az integrandum speciális formája segítségével.

Egy másik lehetőség, hogy egy ismert integrállal kezdjük, és integrációs technikákkal átalakítjuk, amíg meg nem kapjuk a kívánt integrált. Példa:

Ennek meghatározásához részben integráljuk a következő hasonló integrált: ${\ displaystyle \ texttyle \ int {\ frac {\ mathrm {d} x} {(1 + x ^ {2}) ^ {2}}}}$

${\ displaystyle {\ begin {aligned} \ arctan x & = \ int 1 \ cdot {\ frac {1} {1 + x ^ {2}}} \, \ mathrm {d} x \\ & = x \ cdot {\ frac {1} {1 + x ^ {2}}} + \ int x \ cdot {\ frac {2x} {(1 + x ^ {2}) ^ {2}}} \, \ mathrm {d } x \\ & = {\ frac {x} {1 + x ^ {2}}} + \ int \ left ({\ frac {2x ^ {2}} {(1 + x ^ {2}) ^ { 2}}} + {\ frac {2} {(1 + x ^ {2}) ^ {2}}} \ jobb) \, \ mathrm {d} x- \ int {\ frac {2} {(1 + x ^ {2}) ^ {2}}} \, \ mathrm {d} x \\ & = {\ frac {x} {1 + x ^ {2}}} + 2 \ int {\ frac {1 + x ^ {2}} {(1 + x ^ {2}) ^ {2}}} \, \ mathrm {d} x-2 \ int {\ frac {1} {(1 + x ^ {2} ) ^ {2}}} \, \ mathrm {d} x \\ & = {\ frac {x} {1 + x ^ {2}}} + 2 \ arctan x-2 \ int {\ frac {\ mathrm {d} x} {(1 + x ^ {2}) ^ {2}}} \ end {igazítva}}}$

Ennek megváltoztatásával következik

${\ displaystyle \ int {\ frac {\ mathrm {d} x} {(1 + x ^ {2}) ^ {2}}} = {\ frac {1} {2}} \ bal ({\ frac { x} {1 + x ^ {2}}} + \ arctan x \ jobb).}$

Többszörös integráció

Ha egy függvényt többször kell integrálni, akkor a Cauchy -féle többszörös integrációs képlet biztosítja a pontban az iterált integrált${\ displaystyle f}$${\ displaystyle n}$${\ displaystyle f}$${\ displaystyle x}$

${\ displaystyle I ^ {n} (x) = \ int _ {a} ^ {x} \ int _ {a} ^ {\ sigma _ {1}} \ cdots \ int _ {a} ^ {\ sigma _ {n-1}} f (\ sigma _ {n}) \, \ mathrm {d} \ sigma _ {n} \ cdots \, \ mathrm {d} \ sigma _ {2} \, \ mathrm {d} \ sigma _ {1}}$

a következő integrált:

${\ displaystyle I ^ {n} (x) = {\ frac {1} {(n-1)!}} \ int _ {a} ^ {x} \ left (xt \ right) ^ {n-1} f (t) \, \ mathrm {d} t}$.

Alkalmazások

Folyamatos függvények átlagértékei

Annak kiszámításához az átlagos értéke egy adott folytonos függvény egy intervallumon, az egyik használja a képlet ${\ displaystyle m}$ ${\ displaystyle f}$ ${\ displaystyle [a, b]}$

${\ displaystyle m = {\ frac {1} {ba}} \ int _ {a} ^ {b} f (x) \ mathrm {d} x.}$

Mivel ez a meghatározás a lépcsőfunkciókhoz megfelel az átlagos érték szokásos fogalmának, ez az általánosítás hasznos.

Az integrálszámítás átlagérték -tétele azt mondja, hogy ezt az átlagértéket valójában az intervallum folytonos függvénye feltételezi. ${\ displaystyle [a, b]}$

Példa az integrál kifejezésre a fizikában

A fizikai jelenség , hogy lehet használni, hogy magyarázza a koncepció integrál a szabadesés a test az a Föld gravitációs mező . A gyorsulás a szabadesés a Közép-Európában kb. 9,81 m / s². A sebesség egy test egy időben ezért kifejezhető a következő képlettel ${\ displaystyle g}$ ${\ displaystyle v}$${\ displaystyle t}$

${\ displaystyle v = g \ cdot t}$

kifejezni.

De most ki kell számítani azt a távolságot, amelyet a leeső test egy bizonyos időn belül megtesz . A probléma itt az, hogy a test sebessége idővel növekszik. Hogy oldja meg a problémát, azt feltételezzük, hogy egy rövid ideig a sebességet , ami az idő állandó marad. ${\ displaystyle l}$${\ displaystyle T}$${\ displaystyle v}$${\ displaystyle \ Delta t}$${\ displaystyle v}$${\ displaystyle g \ cdot t}$

A rövid időn belül megtett távolság növekedése tehát ${\ displaystyle \ Delta t}$

${\ displaystyle \ Delta l = g \ cdot t \, \ cdot \ Delta t}$.

A teljes távolság tehát leírható

${\ displaystyle l = \ összeg \ bal (g \ cdot t \, \ cdot \ Delta t \ right)}$

kifejezni. Ha most megengedi, hogy az időkülönbség nulla felé hajlik, akkor megkapja ${\ displaystyle \ Delta t}$

${\ displaystyle l = \ lim _ {\ Delta t \ to 0} \ left (\ sum \ left (g \ cdot t \, \ cdot \ Delta t \ right) \ right) = \ int _ {0} ^ { T} \ bal (g \ cdot t \; \ mathrm {d} t \, \ jobb).}$

Az integrál analitikusan megadható a -vel

${\ displaystyle l = \, {\ frac {g} {2}} \ cdot T ^ {2}.}$

Az általános megoldás ahhoz vezet, hogy a test mozgási egyenlete az állandó gravitációs mezőbe esik:

${\ displaystyle l = {\ frac {g} {2}} \ cdot t ^ {2}}$

Továbbá ebből a mozgási egyenletből az idő szerinti differenciálással a sebesség egyenlete a következő lehet:

${\ displaystyle v = g \ cdot t}$

és származzon a gyorsulás ismételt megkülönböztetésével:

${\ displaystyle a = g}$

További egyszerű példák a következők:

• Az energia az erő szerves része az idő múlásával.
• Az elektromos töltés a kondenzátor is integrálja a jelenlegi áramlik rajta keresztül az idők során.
• A szerves termék a spektrális besugárzott felületi teljesítmény ( E _e (ν) a W / m ² Hz ) a spektrális fény érzékenységi görbéjét a szem biztosítja a megvilágítás ( E in lux = lumen / m ² ).
• Az áramlási sebesség integrálja (hosszanti komponens) a cső keresztmetszetén keresztül biztosítja a teljes térfogatáramot a csövön keresztül (további többdimenziós integrálokat lásd alább ).

Konstrukciók

Cauchy integrál

A vezérlőfunkció egy olyan funkció, amelyet a lépésfunkciók segítségével egyenletesen közelíteni lehet . Az integrál fentebb említett kompatibilitása miatt egységes korlátokkal, egy vezérlőfunkció esetében, amely egy lépésfüggvénysorozat egységes határa , az integrált úgy definiálható, hogy ${\ displaystyle f}$${\ displaystyle t_ {n}}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = \ lim _ {n \ to \ infty} \ int _ {a} ^ {b} t_ {n} (x) \, \ mathrm {d} x,}$

ahol a lépésfunkciók integrálját a fent megadott képlet határozza meg.

Az osztály ellenőrzési funkciók tartalmazza az összes folytonos függvények és minden monoton függvény , valamint az összes funkció , amelyre lehet bontani a véges sok időközönként , hogy a korlátozás az , hogy folyamatos vagy monoton függvény a zárt intervallum , azaz H. minden darabonkénti folyamatos funkció. Ez magában foglalja a korlátozott variációjú funkciókat is, mivel egy ilyen függvény két monoton növekvő függvény közötti különbségként ábrázolható. Ez az integrált konstrukció sok gyakorlati célra teljesen elegendő. ${\ displaystyle f}$${\ displaystyle [a, b]}$${\ displaystyle I_ {k}}$${\ displaystyle f}$${\ displaystyle I_ {k}}$${\ displaystyle {\ bar {I}} _ {k}}$

Vannak folyamatos funkciók is végtelen variációkkal, mint pl B. A függvény által és számára az intervallum (lásd variáció ). ${\ displaystyle 0 \ mapsto 0}$${\ displaystyle t \ mapsto t \ cos {\ tfrac {\ pi / 2} {t}}}$${\ displaystyle 0 <t \ leq 1}$${\ displaystyle [0,1]}$

Riemann integrál

Az egyik megközelítés, hogy a számítás a szerves szerinti Riemann a közelítése a funkciót kell integrálni egy lépcsős függvény ; azonban nem magának a függvénynek az egységes közelítésével, hanem a terület közelítésével téglalap alakú összegekkel.

A területet az egyes "lépcsők" alatti egyes téglalapok területének összege közelíti meg . Az integrációs intervallum minden egyes bontásához kiválaszthatja az egyes részintervallumok bármelyik funkcióértékét a szint szintjeként.

Ezek után a német matematikus Bernhard Riemann úgynevezett Riemann összegek. Ha valaki a függvény felsőbbségét választja a téglalap magasságának a bontás minden részintervallumában , akkor a felső összeg jön létre , a legkevesebb pedig az alsó összeg.

A Riemann integrál felső és alsó összegek segítségével határozható meg, lásd Riemann integrál. Ha a felső és az alsó összeg azonos határértékhez konvergál , akkor ez a határérték a Riemann -értelemben vett integrál. Ebben az értelemben integrálhatóak a z. B. minden olyan funkció, amelyhez a Cauchy integrál létezik.

A Riemann -integrál létezik pl. B. nem az intervallumban található racionális számok indikátorfüggvényére , azaz. H. a Dirichlet -függvényhez . Ezért Henri Léon Lebesgue ( Lebesgue -integrál ), Thomas Jean Stieltjes ( Stieltjes -integrál ) és Haar Alfréd kiterjesztett integrál kifejezéseket vezetett be , amelyek a Riemann -integrált reprodukálják a folyamatos integrációkhoz. ${\ displaystyle [0,1]}$

Stieltjes integrál

A Stieltjes-integrál monoton , vagy véges variációjú , azaz két monoton függvény közötti különbségeken alapul, a Riemann-Stieltjes-összegeket pedig folytonos függvényekre határozzák meg , ${\ displaystyle g (x)}$${\ displaystyle f}$

${\ displaystyle \ sum _ {i = 0} ^ {n -1} \, f (x_ {i}) \, \ {g (x_ {i + 1}) - g (x_ {i}) \}. }$

Ezután az úgynevezett Riemann-Stieltjes integrált úgy kapjuk meg, hogy a szokásos módon határokat alakítunk ki . ${\ displaystyle \ texttyle \ int _ {I} \, f \, \ mathrm {d} g}$

Az ilyen integrálok akkor is definiáltak, ha a függvény nem differenciálható (egyébként érvényes ). Jól ismert ellenpélda az úgynevezett Heaviside függvény , amelynek értéke negatív számoknál nulla, pozitív és z. B. a lényegre . Az ember ír és így kapja meg az „általánosított függvényt” , az úgynevezett Dirac-mértéket , mint olyan mértéket , amely csak a lényegre vonatkozik . ${\ displaystyle g}$${\ displaystyle \ mathrm {d} g \ equiv g '(x) \, \ mathrm {d} x}$ ${\ displaystyle \ Theta (x)}$${\ displaystyle x}$${\ displaystyle = 1/2}$${\ displaystyle x = 0}$${\ displaystyle g (x) = \ Theta (x),}$ ${\ displaystyle \ mathrm {d} g = \ delta (x) \ mathrm {d} x}$ ${\ displaystyle \ delta (x)}$${\ displaystyle x = 0}$

Lebesgue integrálja

A Lebesgue integrál modernebb és sok szempontból jobb integrált kifejezést nyújt, mint a Riemann integrál. Például lehetővé teszi az integrációt általános dimenziós terek használatával . Ez azt jelenti, hogy a mennyiségekhez hozzá lehet rendelni egy olyan mértéket, amelynek nem feltétlenül kell megegyeznie geometriai hosszával vagy térfogatával, például valószínűségmérések a valószínűségelméletben . A hossz vagy térfogat intuitív fogalmának megfelelő mérték a Lebesgue -mérték . A dimenzió feletti integrált általában Lebesgue integrálnak nevezik . Bizonyítható, hogy minden olyan funkcióhoz, amely Riemann integrálható egy kompakt intervallumban, létezik a megfelelő Lebesgue integrál is, és mindkét integrál értéke megegyezik. Ezzel szemben nem minden Lebesgue-integrálható függvény szintén Riemann-integrálható. A legismertebb példa erre a Dirichlet-függvény , vagyis az a függvény, amelynek racionális számok esetén az értéke 1, de az irracionális számoké nulla. Amellett, hogy a nagyobb osztályában integrálható függvények, a Lebesgue integrál az különbözteti meg a Riemann-integrál elsősorban a jobb konvergencia tételek ( tétele monoton konvergencia , tétele majorized konvergencia ), valamint a jobb tulajdonságait funkció terek normalizálta a Lebesgue integrál ( nagyjából a teljesség ).

A modern matematikában az integrált vagy integrációs elméletet gyakran Lebesgue integrál fogalmának tekintik.

Helytelen integrál

A Riemann-integrál (egydimenziós térben) csak kompakt , azaz korlátozott és zárt intervallumokra van definiálva . A helytelen integrál általánosítást kínál a definíció korlátlan tartományaira vagy szingularitású funkciókra . A Lebesgue -elméletben a nem megfelelő integrálok is figyelembe vehetők, de ez nem olyan produktív, mivel a Lebesgue -integrál sok funkciót integrálhat szingularitással vagy korlátlan tartományba.

Határozott és helytelen integrálok számítási módszere

Numerikus módszerek

Gyakran nehéz vagy lehetetlen kifejezetten meghatározni egy antiderivatívumot. Sok esetben azonban elegendő hozzávetőlegesen kiszámítani az adott integrált. Azután beszélünk numerikus kvadratúráról vagy numerikus integrációról . A numerikus kvadratúra számos módszere a függvény közelítésén alapul, amely könnyebben integrálható függvényekkel, például polinomokkal. A trapezoid szabály vagy Simpson-féle képlet (a speciális esetben, amely ismert a Kepler hordó szabály ) példák erre, itt egy interpolációs polinomot helyezzük a funkciót , majd az integrált.

Jóval a számítógépek elterjedése előtt kidolgozták az automatikus lépésméret -szabályozási módszereket a numerikus integrációhoz . Manapság a számítógépes algebra lehetőséget kínál komplex integrálok számszerű megoldására egyre rövidebb idő alatt vagy egyre pontosabb megoldásokkal, így még nagy teljesítményű rendszerek esetén is nehézségek merülnek fel a helytelen integrálokkal, amelyek kiszámításához gyakran speciális módszerek, mint például a Gauss-Kronrod használt. Példa egy ilyen kemény integrálra:

${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {\ ln (1 + x)} {\ ln ^ {2} x + \ pi ^ {2}}} \ cdot {\ frac {\ mathrm {d} x} {x ^ {2}}} = \ gamma}$

A klasszikus módszerek pl. B. Euler empirikus formulája , amelyben a határozott integrált egy általánosan aszimptotikus sorozat közelíti. Más módszerek a különbségek számításának elméletén alapulnak, itt fontos példát kell említeni Gregory integrációs képletére.

Pontos eljárások

Számos módszer létezik, amelyekkel határozott és helytelen integrálokat pontosan szimbolikus formában lehet kiszámítani.

Ha folyamatos és antiderivatívum ismert, akkor a határozott integrál lehet ${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle F}$

${\ displaystyle \ int _ {a} ^ {b} f (x) \, \ mathrm {d} x = F (b) -F (a)}$

a főmondat alapján kell kiszámítani. A probléma az, hogy a határozatlan integráció működése adott funkcionális osztályok kiterjesztéséhez vezet. Például a racionális függvények osztályán belüli integráció nem teljes, és a függvényekhez és . Az úgynevezett elemi függvények osztálya sem zárt. Így Joseph Liouville bebizonyította, hogy a függvénynek nincs elemi antiderivatív hatása. Leonhard Euler az elsők között dolgozott ki módszereket bizonyos és helytelen integrálok pontos kiszámítására anélkül, hogy antiderivatívumot határozna meg. Az idő múlásával számos általánosabb és specifikusabb integrációs módszer alakult ki: ${\ displaystyle \ ln}$${\ displaystyle \ arctan}$${\ displaystyle e ^ {- x ^ {2}}}$

• A reziduális tétel felhasználásával
• Az integrál ábrázolása paramétertől függően speciális funkciókat használva
• Az integrál differenciálása vagy integrálása egy paraméter szerint és a határfolyamatok felcserélése
• Az integráns sorozat kibővítésének használata az egyesítésekkel
• részleges integráció és helyettesítés révén csökkenti az integrált önmagának vagy másnak

A 20. század végére számos (néha többkötetes) integráltáblát hoztak létre bizonyos integrálokkal. Néhány példa a probléma szemléltetésére:

${\ displaystyle \ int _ {0} ^ {1} {\ frac {\ ln (1 + x)} {x ^ {2} +1}} \, \ mathrm {d} x = {\ frac {\ pi } {8}} \ 2.$

${\ displaystyle \ int _ {0} ^ {\ pi} \ ln \ sin x \, \ mathrm {d} x = - \ pi \ ln 2}$

Különleges integrálok

Számos határozott és helytelen integrál létezik, amelyek bizonyos jelentéssel bírnak a matematika számára, és ezért saját nevük van:

• Euler integrálok az első és a második fajta
• Gauss -hiba integrál

${\ displaystyle \ int _ {- \ infty} ^ {\ infty} e ^ {- t ^ {2}} \, \ mathrm {d} t = {\ sqrt {\ pi}}}$

• Fresnel integrálok

${\ displaystyle \ int _ {0} ^ {\ infty} \ cos t ^ {2} \, \ mathrm {d} t = \ int _ {0} ^ {\ infty} \ sin t ^ {2} \, \ mathrm {d} t = {\ tfrac {1} {4}} {\ sqrt {2 \ pi}}}$

• Raabe szerves része

${\ displaystyle \ int \ limits _ {a} ^ {a + 1} \ log \ Gamma (t) \, \ mathrm {d} t = {\ tfrac {1} {2}} \ log 2 \ pi + a \ log aa, \ quad a \ geq 0,}$   és főleg az , és  :${\ displaystyle a = 0}$${\ displaystyle a = e}$${\ displaystyle \ int _ {0} ^ {1} \ log \ Gamma (t) \, \ mathrm {d} t = {\ tfrac {1} {2}} \ log 2 \ pi}$

• Frullan integrálok

${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {f (ax) -f (bx)} {x}} \, \ mathrm {d} x}$

Többdimenziós integráció

Útintegrálok

Valódi útintegrálok és görbe hossza

Ha van egy útvonal , azaz a folyamatos feltérképezése, és egy skalár függvény, akkor a pályaintegrál a mentén van definiáljuk ${\ displaystyle \ gamma \ kettőspont [a, b] \ to \ mathbb {R} ^ {n}}$${\ displaystyle f \ colon \ mathbb {R} ^ {n} \ to \ mathbb {R}}$${\ displaystyle f}$${\ displaystyle \ gamma}$

${\ displaystyle \ int _ {\ gamma} f (x) \, \ mathrm {d} x = \ int _ {a} ^ {b} f (\ gamma (t)) \, \ | {\ dot {\ gamma}} (t) \ | \, \ mathrm {d} t.}$

Ha a fenti képletből megkapjuk a görbe hosszát (fizikailag), mint a sebesség integrálját az idő múlásával: ${\ displaystyle f \ equiv 1}$${\ displaystyle \ gamma \ kettőspont [a, b] \ to \ mathbb {R} ^ {2}}$

${\ displaystyle L (\ gamma) = \ int _ {a} ^ {b} \ | {\ dot {\ gamma}} (t) \ | \, \ mathrm {d} t = \ int _ {a} ^ {b} {\ sqrt {{\ dot {x}} (t) ^ {2} + {\ pont {y}} (t) ^ {2}}} \, \ mathrm {d} t}$

Valós útintegrálok a vektorfüggvényekhez

A fizikában gyakran használják a következő alakú útintegrálokat: vektorfüggvény , és ez lesz az integrál ${\ displaystyle {\ vec {f}}}$${\ displaystyle \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {n}}$

${\ displaystyle \ int _ {\ gamma} {\ vec {f}} (x) \ cdot \ mathrm {d} x = \ int _ {a} ^ {b} \ langle {\ vec {f}} (\ gamma (t)), {\ dot {\ gamma}} (t) \ rangle \, \ mathrm {d} t}$

ahol a szögletes zárójelben lévő kifejezés skaláris szorzat .

Komplex útintegrálok

A függvényelméletben , azaz az elemzés kiterjesztésében egy komplex változó függvényeire, már nem elegendő az integráció alsó és felső határának megadása. A számegyenes két pontjától eltérően a komplex sík két pontja sokféleképpen összekapcsolható egymással. Ezért a függvényelmélet határozott integrálja alapvetően útintegrál . A reziduális tétel a zárt utakra vonatkozik , Cauchy fontos eredménye: A meromorf függvény integrálja a zárt út mentén kizárólag a zárt szingularitások számától függ. Nulla, ha nincsenek szingularitások az integrációs területen.

Felületi integrálok

Példa: A szoba tartalmának kiszámítása

Példaként, a térfogata közötti a grafikont a funkció számítjuk azzal az egységnyi oldalú négyzet . Ehhez az integrált két integrálra osztja , egyet a - és egyet a koordinátára: ${\ displaystyle f \ colon \ mathbb {R} ^ {2} \ to \ mathbb {R}}$${\ displaystyle f (x, y): = x ^ {2} + y}$ ${\ displaystyle I: = [0,1] \ alkalommal [0,1]}$${\ displaystyle I}$${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle {\ begin {aligned} \ int _ {[0,1] \ times [0,1]} f (x, y) \, \ mathrm {d} (x, y) & = \ int _ { 0} ^ {1} \ int _ {0} ^ {1} f (x, y) \, \ mathrm {d} x \, \ mathrm {d} y = \ int _ {0} ^ {1} \ int _ {0} ^ {1} (x ^ {2} + y) \, \ mathrm {d} x \, \ mathrm {d} y \\ & = \ int _ {0} ^ {1} \ bal [{\ tfrac {1} {3}} x ^ {3} + yx \ right] _ {x = 0} ^ {1} \, \ mathrm {d} y = \ int _ {0} ^ {1} \ balra ({\ tfrac {1} {3}} + y \ jobb) \ mathrm {d} y = \ balra [{\ tfrac {1} {3}} y + {\ tfrac {1} {2}} y ^ {2} \ right] _ {y = 0} ^ {1} = {\ tfrac {5} {6}} \ end {aligned}}}$

A felületi integrál megadja az integrációs felület területét. ${\ displaystyle f \ equiv 1}$

Kötetintegrálok

A kötetintegrál kiszámítja az integrációs terület térfogattartalmát. ${\ displaystyle f \ equiv 1}$

Integráció többdimenziós és magasabb dimenziós területek között

Az integrál fogalmát általánosítani lehet arra az esetre, hogy a hordozóhalmaz, amelyen az integráns működik, nem a számegyenes , hanem a -dimenziós euklideszi tér . ${\ displaystyle f}$${\ displaystyle \ mathbb {R}}$${\ displaystyle n}$ ${\ displaystyle \ mathbb {R} ^ {n}}$

Fubini -tétel és transzformációs tétel

A többdimenziós integrálok, azaz a terület- és térfogati integrálok esetében Fubini-tételt használunk, amely lehetővé teszi az integrálok tetszőleges sorrendben történő felosztását az egyes koordináták között, és egymás utáni feldolgozását:

${\ displaystyle {\ begin {aligned} \ int _ {V} f \ left ({\ vec {r}} \ right) \ mathrm {d} ^ {3} r & = \ iiint f (x, y, z ) \ mathrm {d} z \, \ mathrm {d} y \, \ mathrm {d} x \\ & = \ int \ left (\ int \ left (\ int f (x, y, z) \ mathrm { d} z \ jobb) \ mathrm {d} y \ jobb) \ mathrm {d} x \ end {igazítva}}}$

Az egydimenziós integrálok integrálási korlátai , és a hangerő korlátozásából kell meghatározni . Az egydimenziós helytelen integrálokhoz hasonlóan (lásd fent) az egész, korlátlan dimenziós tér integráljait is figyelembe lehet venni . ${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle z}$${\ displaystyle V}$${\ displaystyle n}$

A multidimenzionális helyettesítési szabály általánosítása az átalakítási tétel . Legyen nyitott és egy injektıv , folytonosan differenciálható leképezést, akinek a funkcionális meghatározó valamennyi . Azután ${\ displaystyle \ Omega \ részhalmaz \ mathbb {R} ^ {d}}$ ${\ displaystyle \ Phi \ colon \ Omega \ to \ mathbb {R} ^ {d}}$ ${\ displaystyle \ det (D \ Phi (x)) \ neq 0}$${\ displaystyle x \ in \ Omega}$

${\ displaystyle \ int _ {\ Phi (\ Omega)} f (y) \, \ mathrm {d} y = \ int _ {\ Omega} f (\ Phi (x)) \ bal | \ det (D \ Phi (x)) \ jobb | \ mathrm {d} x.}$

Integrálok az elosztók felett

A terület felszínén történő integráció különösen érdekes számos fizikai alkalmazásban. Az ilyen felületeket általában elosztók írják le . Ezeket úgynevezett térképek írják le.

Integráció térképi területen

Hagy egy dimenziós submanifold a és egy térképet a területen , vagyis a nyílt részhalmaza , amelynek van egy térkép , amely feltérképezi az diffeomorphically nyílik egy nyitott részhalmaza . Továbbá hagyjuk a paraméterezést , azaz egy folyamatosan differenciálható leképezést, amelynek levezetése teljes rangú, és homeomorf módon leképeződik. Ezután a függvény integrálja a térképterületen a következő: ${\ displaystyle M}$${\ displaystyle d}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle U}$${\ displaystyle M}$${\ displaystyle M}$${\ displaystyle \ mathbb {R} ^ {d}}$${\ displaystyle \ gamma \ colon \ Omega \ to U}$${\ displaystyle U}$${\ displaystyle \ Omega}$ ${\ displaystyle \ gamma (\ Omega)}$${\ displaystyle U}$

${\ displaystyle \ int _ {U} f \ mathrm {d} s: = \ int _ {\ Omega} f (\ gamma (u)) {\ sqrt {g ^ {\ gamma} (u)}} \ mathrm {d} u,}$

hol a Gram meghatározója . A megfelelő integrál kiszámítható a fent leírt többdimenziós integrációs módszerekkel. Az egyenlőség lényegében a transzformációs tételből következik. ${\ displaystyle g ^ {\ gamma} (u) = \ det ((\ gamma '(u)) ^ {\ mathsf {T}} \ cdot \ gamma' (u))}$

Integráció alosztályon keresztül

Ha van 1 bontás , amely kompatibilis az alosztály térképével, akkor egyszerűen integrálható és külön összeadható a térképterületeken.

A Gauss -integrál tétel és a Stokes -tétel

Speciális funkciók esetén az integrálok könnyebben kiszámíthatók az alosztályok segítségével. Két megállapítás különösen fontos a fizikában:

Egyrészt létezik a Gauss -féle integrál -tétel , amely szerint a vektormező divergenciája feletti térfogatintegrál egyenlő a vektormező feletti felületi integrállal (a mező áramlása a felszínen): Legyen tömör , sima él szakaszokban . Hagyja, hogy az él külső normál egységmezővel legyen irányítva . Továbbá legyen egy folyamatosan differenciálható vektormező egy nyílt környéken . Akkor érvényes ${\ displaystyle V \ részhalmaz \ mathbb {R} ^ {n}}$ ${\ displaystyle \ partial V}$${\ displaystyle {\ vec {n}}}$${\ displaystyle {\ vec {F}}}$${\ displaystyle V}$

${\ displaystyle \ int _ {V} \ operatornév {div} {\ vec {F}} \, \ mathrm {d} ^ {(n)} V = \ oint _ {\ részleges V} {\ vec {F} } \ cdot \ mathrm {d} ^ {(n-1)} {\ vec {S}}}$

a rövidítéssel . ${\ displaystyle \ mathrm {d} ^ {(n-1)} {\ vec {S}} = {\ vec {n}} \, \ mathrm {d} ^ {(n-1)} S}$

Ez a mondat úgy értelmezi a divergencia, mint az úgynevezett forrás sűrűsége vektor területen. A megfelelő integrációs elosztó dimenzióját az indexek vagy a kezelő is hangsúlyozza. ${\ displaystyle (n)}$${\ displaystyle (n-1)}$${\ displaystyle \ mathrm {d}}$

Ha több integrált használ kifejezetten (indexelés nélkül) a következőkre : ${\ displaystyle n = 3}$

${\ displaystyle \ iiint _ {V} \ operatornév {div} \, {\ vec {F}} ({\ vec {x}}) \, \ mathrm {d} V = \ iint _ {\ részleges V} { \ vec {F}} \ cdot \ mathrm {d} {\ vec {S}}}$

Tehát: A divergencia integrálja a teljes térfogatban egyenlő a felszínről érkező áramlás integráljával.

Másodszor, Stokes tétele , amely a differenciálgeometria megállapítása, és a háromdimenziós tér különleges esetére, több integrállal közvetlenül írható.

Ha létezik egy háromdimenziós euklideszi tér kétdimenziós részhalmaza , akkor érvényes ${\ displaystyle M}$ ${\ displaystyle \ mathbb {R} ^ {3}}$

${\ displaystyle \ iint _ {M} \ operatornév {rot} {\ vec {F}} \ cdot \ mathrm {d} {\ vec {S}} = \ int _ {\ részleges M} {\ vec {F} } \ cdot \ mathrm {d} {\ vec {r}},}$

ahol jelöli a forgását a vektor mező . ${\ displaystyle \ operatornév {red} {\ vec {F}}}$${\ displaystyle {\ vec {F}}}$

Ez a mondat a vektormező forgását a vektormező úgynevezett örvénysűrűségének értelmezi ; ahol a három komponensű vektor és a szélén a zárt görbe im . ${\ displaystyle \ mathrm {d} {\ vec {r}}}$${\ displaystyle (\ mathrm {d} x, \ mathrm {d} y, \ mathrm {d} z)}$${\ displaystyle \ partial M}$${\ displaystyle M}$${\ displaystyle \ mathbb {R} ^ {3}}$

Vektor értékű függvények integrálása

Az olyan funkciók integrálása, amelyek nem valósak vagy összetett értékűek, de értékeket vesznek fel egy általánosabb vektor térben, szintén sokféleképpen lehetséges.

A Lebesgue-integrál Banach űrértékfüggvényekhez való közvetlen általánosítása a Bochner-integrál ( Salomon Bochner után ). Az egydimenziós elmélet számos eredménye szó szerint átkerül Banach-terekbe.

A Riemann-integrál definíciójának átvitele vektor-értékű függvényekbe Riemann-összegek használatával szintén nem nehéz. Lényeges különbség azonban az, hogy ekkor nem minden Riemann-integrálható függvény lehet Bochner-integrálható. ${\ displaystyle f \ colon [a, b] \ to V}$

A Bochner és Riemann integrálok általános általánosítása, amely ezt a hiányt leküzdi, a McShane integrál , amelyet a legegyszerűbben általánosított Riemann -összegek segítségével lehet meghatározni.

A Birkhoff -integrál a Bochner- és Riemann -integrál általános általánosítása is. A McShane -integrállal ellentétben azonban a Birkhoff -integrál meghatározása nem igényel topológiai struktúrát a függvények meghatározási területén. Ha azonban a McShane integráció követelményei teljesülnek, akkor minden Birkhoff-integrálható funkció is lehet McShane-integrálható.

Ezenkívül a Pettis integrált érdemes megemlíteni a következő általánosítási lépésként. Ez használ egy funkcionális elemzési meghatározás, amelyben az integrálhatóság csökken az egydimenziós eset: Legyen egy intézkedés helyet . Egy függvényt Pettis-integrálhatónak nevezünk, ha a Lebesgue-integrálható függvény minden folyamatos függvényre, és minden mérhető halmazra létezik vektor , így ${\ displaystyle (\ Omega, {\ mathcal {A}}, \ mu)}$${\ displaystyle f \ colon \ Omega \ to V}$${\ displaystyle \ lambda \ in V '}}$${\ displaystyle \ lambda \ circ f \ colon \ Omega \ to \ mathbb {R}}$${\ displaystyle A \ in {\ mathcal {A}}}$${\ displaystyle x_ {A} \ in V}$

${\ displaystyle \ forall \ lambda \ in V '\ colon \ \ lambda (x_ {A}) = \ int _ {A} {\ lambda \ circ f} \, \ mathrm {d} \ mu}$

alkalmazandó. A vektort ezután megfelelően megjelöljük. ${\ displaystyle x_ {A}}$${\ displaystyle \ texttyle \ int _ {A} f \, \ mathrm {d} \ mu}$

Azon funkciók esetében , amelyek értékeket különálló Banach -térben vesznek fel , a Pettis integrál megegyezik a McShane és Bochner integrálokkal. Mindezen definíciók legfontosabb speciális esete a függvények esete , amelyek egyszerűen komponensenként vannak integrálva ezekbe a definíciókba. ${\ displaystyle f \ colon [a, b] \ to V}$${\ displaystyle V}$${\ displaystyle \ mathbb {R} ^ {n}}$

Általánosítások

Az integrál kifejezést sokféleképpen kibővítették, néhány változat:

• Riemann integrál
• Daniell integrál
• Stieltjes integrál
• Itō integrál és Stratonowitsch integrál , lásd még Diszkrét sztochasztikus integrál
• Mérőintegrál vagy Henstock-Kurzweil integrál , különösen:
  • McShane integrál
  • Bors integrál
• Integrál mérése
  • Lebesgue integrálja
  • Bochner integrál
  • Birkhoff integrál
  • Pettis szerves része
  • Haj szerves
• Volkenborn integrál

Méréselmélet

Szőrös intézkedés

A Haar -mérték Haar Alfréd után a Lebesgue -mérték általánosítását képviseli a helyileg kompakt topológiai csoportokra vonatkozóan, és így egy integrált is indukál a Lebesgue -integrál általánosításaként.

Integráció az elosztócsöveken

Lásd: Differenciálformák integrálása

Végül az integráció az adott testek felületének mérésére is használható. Ez a differenciálgeometria területéhez vezet .

Lásd még

• Algebrai integráció
• Sztochasztikus integráció
• A derivált és antiderivatív függvények táblázata
• Volkenborn integrál

irodalom

• Tankönyvek:
  • Az integrált számítás a középfokú oktatás központi tárgya, ezért minden matematikai tankönyvben foglalkoznak vele.
• Tankönyvek matematika és kapcsolódó tárgyak (fizika, informatika) hallgatói számára:
  • Herbert Amann, Joachim Escher : Elemzés I, II, III. Birkhäuser-Verlag Basel Boston Berlin, ISBN 3-7643-7755-0 , ISBN 3-7643-7105-6 , ISBN 3-7643-6613-3 .
  • Richard Courant : Előadások a differenciál- és integrálszámításról 1, 2. Springer, 1. kiadás 1928, 4. kiadás 1971.
  • Gregor Michailowitsch Fichtenholz : Differenciál- és integrálszámítás I - III. Harri Deutsch kiadó, Frankfurt am Main, 1990–2004. ISBN 978-3-8171-1418-4 (teljes készlet).
  • Forster Ottó : Elemzés 1. Egy változó differenciál- és integrálszámítása. 7. kiadás, Vieweg-Verlag, 2004. ISBN 3-528-67224-2 .
  • Forster Ottó: Elemzés. 3. kötet: Mérték- és integrációs elmélet, integrált tételek az R ⁿ -ben és az alkalmazásokban , 8. javított kiadás. Springer Spectrum, Wiesbaden, 2017, ISBN 978-3-658-16745-5 .
  • Konrad Königsberger : Elemzés. 2 kötet, Springer, Berlin 2004.
  • Vlagyimir Ivanovics Szmirnov : Felső matematika tanfolyam (1–5. Rész). Harri Deutsch kiadó, Frankfurt am Main, 1995–2004. ISBN 978-3-8171-1419-1 (teljes készlet).
  • Steffen Timmann: Repetitorium der Analysis 1, 2. 1. kiadás. Binomi Verlag, 1993.
• Tankönyvek matematika al- / alaptantárgyú diákoknak (pl. Mérnöki vagy közgazdász hallgatók):
  • Rainer Ansorge és Hans Joachim Oberle: Matematika mérnököknek. 1. kötet 3. kiadás. Wiley-VCH, 2000.
  • Lothar Papula : Matematika természettudósoknak és mérnököknek. 1. kötet 13. kiadás. Vieweg + Teubner Verlag. ISBN 978-3-8348-1749-5 .
• Történelmi:
  • Adolph Mayer: Hozzájárulás az egyszerű integrálok maximumának és minimumának elméletéhez. Teubner, Lipcse 1866 ( digitalizált változat ).
  • Bernhard Riemann: Egy függvény trigonometrikus sorozat által való ábrázolhatóságáról. Göttingen 1867 ( teljes szöveg ), a Riemann -integrál első meghatározásával (12. oldal és később).

web Linkek

• Online számológép integrálok (antiderivatívumok) kiszámításához, számítási módszerrel és magyarázatokkal (német)
• mathe-online.at - Erőforrások az integráció témájában (2. másodlagos szint / FHS / Uni)
• Világos magyarázatok
• Az integrátor - angol oldal az integrálok kiszámításához
• Integrált számológép - német webhely a határozott és határozatlan integrálok (antiderivatívumok) kiszámításához
• A háromrészes sorozat 1. része több integrálról (részletes + kiterjedt)
• 50 példa a gyökér függvényekre
• Videó: integrált, antiderivatív . Jörn Loviscach 2010, elérhetővé tette a Műszaki Információs Könyvtár (TIB), doi : 10.5446 / 9752 .
• Videó: derivált, integrál, véletlen . Jörn Loviscach 2010, elérhetővé tette a Műszaki Információs Könyvtár (TIB), doi : 10.5446 / 9736 .
• Videó: határozott integrál 1 . Jörn Loviscach 2010, elérhetővé tette a Műszaki Információs Könyvtár (TIB), doi : 10.5446 / 9755 .
• Videó: határozott integrál 2 . Jörn Loviscach 2010, elérhetővé tette a Műszaki Információs Könyvtár (TIB), doi : 10.5446 / 9756 .

Egyéni bizonyíték

1. ↑ D. Fremlin: A vektor értékű függvények McShane és Birkhoff integrálja. ( Memento 2015. április 28 -tól az Internet Archívumban ).